Year :
1990
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 44 of 44 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
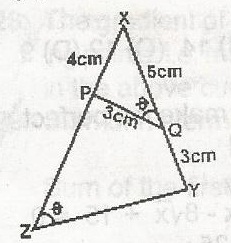 In triangles XYZ and XQP, XP = 4cm, XQ = 5cm and PQ = QY = 3cm. Find ZY A. 8cm B. 6cm C. 4cm D. 3cm |
B |
| 42. |
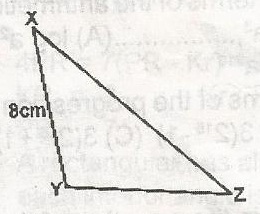 In the figure, YXZ = 30o, XYZ = 105o and XY = 8cm. Calculate YZ A. 16\(\sqrt{2}\)cm B. 8\(\sqrt{2}\)cm C. 4\(\sqrt{2}\)cm D. 22cm Detailed Solutionyzx + 105o + 30o = 180oyzx = 180 - 155 = 45o \(\frac{yz}{sin 30^o} = \frac{8}{sin 45^o}\) yz = \(\frac{8 \sin 30}{sin 45}\) = 8(\(\frac{1}{2}) = \frac{8}{1} \times \frac{1}{2} \times \frac{\sqrt{2}}{1}\) = 4 \(\div\) \(\frac{1}{\sqrt{2}}\) = 4\(\sqrt{2}\)cm |
|
| 43. |
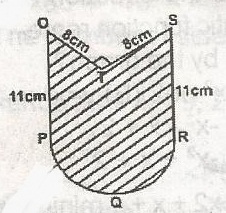 In the figure, PQR is a semicircle. Calculate the area of the shaded region A. 125\(\frac{2}{7}\)2 B. 149\(\frac{2}{7}\)cm2 C. 234\(\frac{1}{7}\)cm2 D. 267\(\frac{1}{2}\)cm2 |
A |
| 44. |
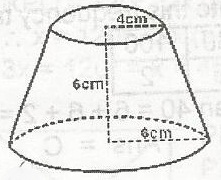 Find the curved surface area of the frustrum in the figure A. 16\(\pi \sqrt{10}\)cm2 B. 20\(\pi \sqrt{10}\)cm2 C. 24\(\pi \sqrt{10}\)cm2 D. 36\(\pi \sqrt{10}\)cm2 Detailed Solution\(\frac{x}{4} = \frac{6 + x}{6}\)6x = 4(6 + x) = 24 + 4x x = 12cm CSA = \(\pi RL - \pi rl\) = \(\pi (6) \sqrt{{18^2} + 6^2} - \pi \times 4 \times \sqrt{{12^2} + 4^2}\) = 6\(\pi \sqrt{360} - 4 \pi \sqrt{160}\) = 36\(\pi \sqrt{10} - 16 \pi \sqrt{10}\) = 20\(\pi \sqrt{10}\)cm2 |
| 41. |
 In triangles XYZ and XQP, XP = 4cm, XQ = 5cm and PQ = QY = 3cm. Find ZY A. 8cm B. 6cm C. 4cm D. 3cm |
B |
| 42. |
 In the figure, YXZ = 30o, XYZ = 105o and XY = 8cm. Calculate YZ A. 16\(\sqrt{2}\)cm B. 8\(\sqrt{2}\)cm C. 4\(\sqrt{2}\)cm D. 22cm Detailed Solutionyzx + 105o + 30o = 180oyzx = 180 - 155 = 45o \(\frac{yz}{sin 30^o} = \frac{8}{sin 45^o}\) yz = \(\frac{8 \sin 30}{sin 45}\) = 8(\(\frac{1}{2}) = \frac{8}{1} \times \frac{1}{2} \times \frac{\sqrt{2}}{1}\) = 4 \(\div\) \(\frac{1}{\sqrt{2}}\) = 4\(\sqrt{2}\)cm |
| 43. |
 In the figure, PQR is a semicircle. Calculate the area of the shaded region A. 125\(\frac{2}{7}\)2 B. 149\(\frac{2}{7}\)cm2 C. 234\(\frac{1}{7}\)cm2 D. 267\(\frac{1}{2}\)cm2 |
A |
| 44. |
 Find the curved surface area of the frustrum in the figure A. 16\(\pi \sqrt{10}\)cm2 B. 20\(\pi \sqrt{10}\)cm2 C. 24\(\pi \sqrt{10}\)cm2 D. 36\(\pi \sqrt{10}\)cm2 Detailed Solution\(\frac{x}{4} = \frac{6 + x}{6}\)6x = 4(6 + x) = 24 + 4x x = 12cm CSA = \(\pi RL - \pi rl\) = \(\pi (6) \sqrt{{18^2} + 6^2} - \pi \times 4 \times \sqrt{{12^2} + 4^2}\) = 6\(\pi \sqrt{360} - 4 \pi \sqrt{160}\) = 36\(\pi \sqrt{10} - 16 \pi \sqrt{10}\) = 20\(\pi \sqrt{10}\)cm2 |