Year :
1990
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 44 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
A cylinder pipe, made of metal is 3cm thick.If the internal radius of the pope is 10cm.Find the volume of metal used in making 3m of the pipe. A. 153\(\pi\)cm3 B. 207\(\pi\)cm3 C. 15 300\(\pi\)cm3 D. 20 700\(\pi\)cm3 Detailed SolutionVolume of a cylinder = πr\(^2\)hFirst convert 3m to cm by multiplying by 100 Volume of External cylinder = π \times 13\(^2\) \times 300 Volume of Internal cylinder = π \times 10\(^2\) \times 300 Hence; Volume of External cylinder - Volume of Internal cylinder Total volume (v) = π (169 - 100) \times 300 V = π \times 69 \times 300 V = 20700πcm\(^3\) |
|
| 32. |
If the heights of two circular cylinder are in the ratio 2 : 3 and their volumes? A. 27 : 32 B. 27 : 23 C. 23 : 32 D. 27 : 23 Detailed Solution\(\frac{h_1}{h_2}\) = \(\frac{2}{3}\)h2 = \(\frac{2h_1}{3}\) \(\frac{r_1}{r_2}\) = \(\frac{9}{8}\) r2 = \(\frac{9r_1}{8}\) v1 = \(\pi\)(\(\frac{9r_1}{8}\))2(\(\frac{2h_1}{3}\)) = \(\pi\)r1 2h1 x \(\frac{27}{32}\) v = \(\frac{\pi r_1 2h_1 \times \frac{27}{32}}{\pi r_1 2h_1}\) = \(\frac{27}{32}\) v2 : v1 = 27 : 32 |
|
| 33. |
The locus of a point which moves so that it is equidistant from two intersecting straight lines is the? A. perpendicular bisector of the two lines B. angle bisector of the two lines C. bisector of the two lines D. line parallel to the two lines Detailed SolutionThe required locus is angle bisector of the two lines |
|
| 34. |
4, 16, 30, 20, 10, 14 and 26 are represented on a pie chart. Find the sum of the angles of the bisectors representing all numbers equals to or greater than 16 A. 48o B. 84o C. 92o D. 276o Detailed SolutionGiven that 4, 16, 30, 20, 10, 14 and 26Adding up = 120 nos \(\geq\) 16 are 16 + 30 + 20 + 26 = 92 The requires sum of angles = \(\frac{92}{120}\) x \(\frac{360^o}{1}\) = 276o |
|
| 35. |
The mean of ten positive numbers is 16. When another number is added, the mean becomes 18. Find the eleventh number A. 3 B. 16 C. 18 D. 38 Detailed SolutionMean of 10 numbers = 16The total sum of numbers = 16 x 10 = 160 Mean of 11 numbers = 18 Total sum of numbers = 11 x 18 = 198 The 11th no. = 198 - 160 = 38 |
|
| 36. |
Below are the scores of a group of students in a test A. 1 B. 2 C. 3 D. 4 Detailed Solution\(\begin{array}{c|c} Scores & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \text{No. of students} & 1 & 4 & 5 & 6 & x & 2\end{array}\)Average = 3.5 3.5 = \(\frac{(1 \times 1) + (2 \times 4) + (3 \times 5) + (4 \times 6) + 5x + (6 \times 2)}{1 + 4 + 5 + 6 + x + 2}\) \(\frac{3.5}{1}\) = \(\frac{1 + 8 + 15 + 24 + 5x + 12}{18 + x}\) \(\frac{3.5}{1}\) = \(\frac{60 + 5x}{18 + x}\) 60 + 5x = 3.5(18 \(\div\) x) 60 + 5x = = 63 + 1.5x 5x - 1.5x = 63 - 60 1.5x = 3 x = \(\frac{3}{1.5}\) \(\frac{30}{15}\) = 2 |
|
| 37. |
Two numbers are removed at random from the numbers 1, 2, 3 and 4. What is the probability that the sum of the numbers removed is even? A. \(\frac{2}{3}\) B. \(\frac{2}{15}\) C. \(\frac{1}{2}\) D. \(\frac{1}{4}\) Detailed Solution\(\begin{array}{c|c} 1 & 2 & 3 & 4\\\hline 1(1, 1) & (1, 2) & (1, 3) & (1, 4)\\ \hline 2(2, 1) & (2 , 2) & (2, 3) & (2, 4) \\ \hline 3(3, 1) & (3, 2) & (3, 3) & (3, 4)\\ \hline 4(4, 1) & (4, 2) & (4, 3) & (4, 4)\end{array}\)sample space = 16 sum of nos. removed are (2), 3, (4), 5 3, (4), 5, (6) (4), 5, (6), 7 (5), 6, 7, (8) Even nos. = 8 of them Pr(even sum) = \(\frac{8}{16}\) = \(\frac{1}{2}\) |
|
| 38. |
Find the probability that a number selected at random from 41 to 56 is a multiply of 9 A. \(\frac{1}{8}\) B. \(\frac{2}{15}\) C. \(\frac{3}{16}\) D. \(\frac{7}{8}\) Detailed SolutionGiven from 41 to 5641, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56 The nos multiple of 9 are: 45, 54 P(multiple of 9) = \(\frac{2}{16}\) = \(\frac{1}{8}\) |
|
| 39. |
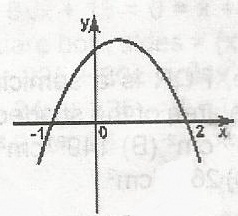 What is the equation of the quadratic function represented by the graph? A. y = x2 + x - 2 B. y = -x2 - x + 2 C. y = x2 - x - 2 D. y = -x2 - x + 2 Detailed SolutionThe required equation is y = x2 - x - 2i.e. B where the graph touches the graph touches the x-axis y = 0 x2 - x - 2 = 0 = (x + 1)(x - 2) = 0 Hence roots of the equation are -1 and 2 as shown in the graph |
|
| 40. |
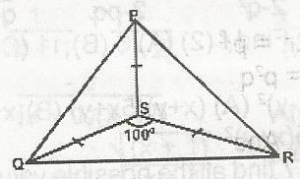 In the figure, PS = QS = RS and QSR - 100o, find QPR A. 40o B. 50o C. 80o D. 100o Detailed SolutionSince PS = QS = RSS is the centre of circle passing through P, Q, R /PS/ = /RS/ = radius QPR \(\pm\) \(\frac{100^o}{2}\) = 50o |
| 31. |
A cylinder pipe, made of metal is 3cm thick.If the internal radius of the pope is 10cm.Find the volume of metal used in making 3m of the pipe. A. 153\(\pi\)cm3 B. 207\(\pi\)cm3 C. 15 300\(\pi\)cm3 D. 20 700\(\pi\)cm3 Detailed SolutionVolume of a cylinder = πr\(^2\)hFirst convert 3m to cm by multiplying by 100 Volume of External cylinder = π \times 13\(^2\) \times 300 Volume of Internal cylinder = π \times 10\(^2\) \times 300 Hence; Volume of External cylinder - Volume of Internal cylinder Total volume (v) = π (169 - 100) \times 300 V = π \times 69 \times 300 V = 20700πcm\(^3\) |
|
| 32. |
If the heights of two circular cylinder are in the ratio 2 : 3 and their volumes? A. 27 : 32 B. 27 : 23 C. 23 : 32 D. 27 : 23 Detailed Solution\(\frac{h_1}{h_2}\) = \(\frac{2}{3}\)h2 = \(\frac{2h_1}{3}\) \(\frac{r_1}{r_2}\) = \(\frac{9}{8}\) r2 = \(\frac{9r_1}{8}\) v1 = \(\pi\)(\(\frac{9r_1}{8}\))2(\(\frac{2h_1}{3}\)) = \(\pi\)r1 2h1 x \(\frac{27}{32}\) v = \(\frac{\pi r_1 2h_1 \times \frac{27}{32}}{\pi r_1 2h_1}\) = \(\frac{27}{32}\) v2 : v1 = 27 : 32 |
|
| 33. |
The locus of a point which moves so that it is equidistant from two intersecting straight lines is the? A. perpendicular bisector of the two lines B. angle bisector of the two lines C. bisector of the two lines D. line parallel to the two lines Detailed SolutionThe required locus is angle bisector of the two lines |
|
| 34. |
4, 16, 30, 20, 10, 14 and 26 are represented on a pie chart. Find the sum of the angles of the bisectors representing all numbers equals to or greater than 16 A. 48o B. 84o C. 92o D. 276o Detailed SolutionGiven that 4, 16, 30, 20, 10, 14 and 26Adding up = 120 nos \(\geq\) 16 are 16 + 30 + 20 + 26 = 92 The requires sum of angles = \(\frac{92}{120}\) x \(\frac{360^o}{1}\) = 276o |
|
| 35. |
The mean of ten positive numbers is 16. When another number is added, the mean becomes 18. Find the eleventh number A. 3 B. 16 C. 18 D. 38 Detailed SolutionMean of 10 numbers = 16The total sum of numbers = 16 x 10 = 160 Mean of 11 numbers = 18 Total sum of numbers = 11 x 18 = 198 The 11th no. = 198 - 160 = 38 |
| 36. |
Below are the scores of a group of students in a test A. 1 B. 2 C. 3 D. 4 Detailed Solution\(\begin{array}{c|c} Scores & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \text{No. of students} & 1 & 4 & 5 & 6 & x & 2\end{array}\)Average = 3.5 3.5 = \(\frac{(1 \times 1) + (2 \times 4) + (3 \times 5) + (4 \times 6) + 5x + (6 \times 2)}{1 + 4 + 5 + 6 + x + 2}\) \(\frac{3.5}{1}\) = \(\frac{1 + 8 + 15 + 24 + 5x + 12}{18 + x}\) \(\frac{3.5}{1}\) = \(\frac{60 + 5x}{18 + x}\) 60 + 5x = 3.5(18 \(\div\) x) 60 + 5x = = 63 + 1.5x 5x - 1.5x = 63 - 60 1.5x = 3 x = \(\frac{3}{1.5}\) \(\frac{30}{15}\) = 2 |
|
| 37. |
Two numbers are removed at random from the numbers 1, 2, 3 and 4. What is the probability that the sum of the numbers removed is even? A. \(\frac{2}{3}\) B. \(\frac{2}{15}\) C. \(\frac{1}{2}\) D. \(\frac{1}{4}\) Detailed Solution\(\begin{array}{c|c} 1 & 2 & 3 & 4\\\hline 1(1, 1) & (1, 2) & (1, 3) & (1, 4)\\ \hline 2(2, 1) & (2 , 2) & (2, 3) & (2, 4) \\ \hline 3(3, 1) & (3, 2) & (3, 3) & (3, 4)\\ \hline 4(4, 1) & (4, 2) & (4, 3) & (4, 4)\end{array}\)sample space = 16 sum of nos. removed are (2), 3, (4), 5 3, (4), 5, (6) (4), 5, (6), 7 (5), 6, 7, (8) Even nos. = 8 of them Pr(even sum) = \(\frac{8}{16}\) = \(\frac{1}{2}\) |
|
| 38. |
Find the probability that a number selected at random from 41 to 56 is a multiply of 9 A. \(\frac{1}{8}\) B. \(\frac{2}{15}\) C. \(\frac{3}{16}\) D. \(\frac{7}{8}\) Detailed SolutionGiven from 41 to 5641, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56 The nos multiple of 9 are: 45, 54 P(multiple of 9) = \(\frac{2}{16}\) = \(\frac{1}{8}\) |
|
| 39. |
 What is the equation of the quadratic function represented by the graph? A. y = x2 + x - 2 B. y = -x2 - x + 2 C. y = x2 - x - 2 D. y = -x2 - x + 2 Detailed SolutionThe required equation is y = x2 - x - 2i.e. B where the graph touches the graph touches the x-axis y = 0 x2 - x - 2 = 0 = (x + 1)(x - 2) = 0 Hence roots of the equation are -1 and 2 as shown in the graph |
|
| 40. |
 In the figure, PS = QS = RS and QSR - 100o, find QPR A. 40o B. 50o C. 80o D. 100o Detailed SolutionSince PS = QS = RSS is the centre of circle passing through P, Q, R /PS/ = /RS/ = radius QPR \(\pm\) \(\frac{100^o}{2}\) = 50o |