Year :
2019
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
41 - 50 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
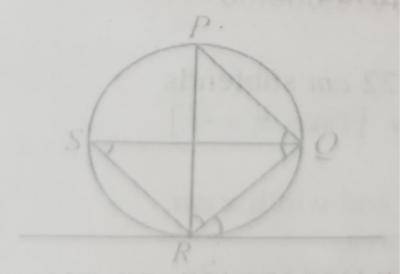 In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Calculate the variance of 2, 4, 7, 8 and 9 A. 7.2 B. 6.8 C. 3.5 D. 2.6 Detailed Solutionx 2 4 7 8 9 (\(\bar{x} - \bar{x}\)) -4 -2 1 2 4 (\(\bar{x} - \bar{x})^2\) 16 4 1 4 9 _________ \(\sum (x - x)^2\) = 34 \(\bar{x} = \frac{2 + 4 + 7 + 8 + 9}{5} = 6 variance = \(\frac{34}{5}\) = 6.8 |
|
| 42. |
The fourth term of an Arithmetic Progression (A.P) is 37 and the first term is -20. Find the common difference. A. 3 B. 57 C. 19 D. 17 Detailed Solutiona + 3d = 37-20 + 3d = 37 3d = 37 + 20 = 57 d = \(\frac{57}{3}\) = 19 |
|
| 43. |
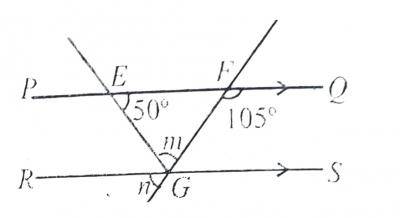 In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of m. A. 130\(^o\) B. 105\(^o\) C. 75\(^o\) D. 55\(^o\) Detailed Solution50\(^o\) + m = 105\(^o\) (exterior angle of \(\triangle\)m = 105\(^o\) - 50\(^o\) m = 55\(^o\) |
|
| 44. |
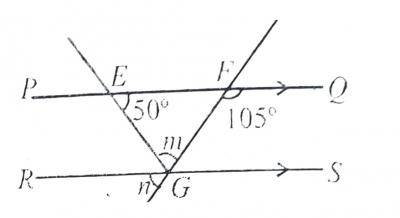 In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of n A. 40\(^o\) B. 55\(^o\) C. 75\(^o\) D. 130\(^o\) Detailed SolutionE\(G\)R = 50\(^o\) (Alternative angles)n + 55\(^o\) + 50\(^o\) = 180\(^o\) (Sum of angles on a straight line) n = 180\(^o\) - 105\(^o\) n = 75\(^o\) |
|
| 45. |
A box contains 5 red, 6 green and 7 yellow pencils of the same size. What is the probability of picking a green pencil at random? A. \(\frac{1}{6}\) B. \(\frac{1}{4}\) C. \(\frac{1}{3}\) D. \(\frac{1}{2}\) Detailed SolutionPr(green) = \(\frac{6}{5 + 6 + 7}\)= \(\frac{6}{18}\) = \(\frac{1}{3}\) |
|
| 46. |
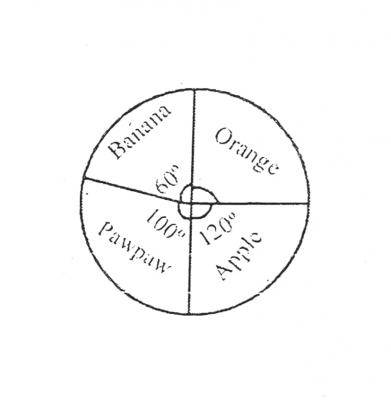 The pie chart represents fruits on display in a grocery shop. If there are 60 oranges on display, how many apples are there? A. 90 B. 80 C. 70 D. 40 Detailed SolutionNo of fruits = x\(\frac{80}{360}\) x \(x\) = 60 x = \(\frac{60 \times 360}{80}\) x 270 = 90 |
|
|
The following are scores obtained by some students in a test. |
||
| 47. |
Find the mode of the distribution A. 18 B. 14 C. 13 D. 8 |
C |
| 48. |
Find the median score A. 14.5 B. 14.0 C. 13.5 D. 13.0 Detailed Solution\(\frac{13 + 14}{2}\) = 13.5 |
|
| 49. |
How many students scored above the mean score? A. 10 B. 9 C. 8 D. 7 Detailed SolutionMean = 13.4No above mean is 7 |
|
| 50. |
Evaluate: \(\frac{0.42 + 2.5}{0.5 \times 2.95}\), leaving the answer in the standard form. A. 1.639 x 10\(^2\) B. 1.639 x 10\(^1\) C. 1.639 x 10\(^{-1}\) D. 1.639 x 10\(^{-2}\) Detailed Solution\(\frac{0.42 \div 2.5}{0.5 \times 2.05} = \frac{0.168}{1.025}\)= 1.639 x 10\(^{-1}\) |
| 41. |
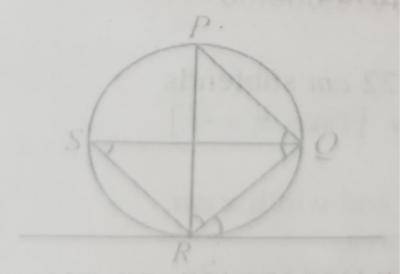 In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Calculate the variance of 2, 4, 7, 8 and 9 A. 7.2 B. 6.8 C. 3.5 D. 2.6 Detailed Solutionx 2 4 7 8 9 (\(\bar{x} - \bar{x}\)) -4 -2 1 2 4 (\(\bar{x} - \bar{x})^2\) 16 4 1 4 9 _________ \(\sum (x - x)^2\) = 34 \(\bar{x} = \frac{2 + 4 + 7 + 8 + 9}{5} = 6 variance = \(\frac{34}{5}\) = 6.8 |
|
| 42. |
The fourth term of an Arithmetic Progression (A.P) is 37 and the first term is -20. Find the common difference. A. 3 B. 57 C. 19 D. 17 Detailed Solutiona + 3d = 37-20 + 3d = 37 3d = 37 + 20 = 57 d = \(\frac{57}{3}\) = 19 |
|
| 43. |
 In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of m. A. 130\(^o\) B. 105\(^o\) C. 75\(^o\) D. 55\(^o\) Detailed Solution50\(^o\) + m = 105\(^o\) (exterior angle of \(\triangle\)m = 105\(^o\) - 50\(^o\) m = 55\(^o\) |
|
| 44. |
 In the diagram, PQ is parallel to RS, < QFG = 105\(^o\) and < FEG = 50\(^o\). Find the value of n A. 40\(^o\) B. 55\(^o\) C. 75\(^o\) D. 130\(^o\) Detailed SolutionE\(G\)R = 50\(^o\) (Alternative angles)n + 55\(^o\) + 50\(^o\) = 180\(^o\) (Sum of angles on a straight line) n = 180\(^o\) - 105\(^o\) n = 75\(^o\) |
|
| 45. |
A box contains 5 red, 6 green and 7 yellow pencils of the same size. What is the probability of picking a green pencil at random? A. \(\frac{1}{6}\) B. \(\frac{1}{4}\) C. \(\frac{1}{3}\) D. \(\frac{1}{2}\) Detailed SolutionPr(green) = \(\frac{6}{5 + 6 + 7}\)= \(\frac{6}{18}\) = \(\frac{1}{3}\) |
| 46. |
 The pie chart represents fruits on display in a grocery shop. If there are 60 oranges on display, how many apples are there? A. 90 B. 80 C. 70 D. 40 Detailed SolutionNo of fruits = x\(\frac{80}{360}\) x \(x\) = 60 x = \(\frac{60 \times 360}{80}\) x 270 = 90 |
|
|
The following are scores obtained by some students in a test. |
||
| 47. |
Find the mode of the distribution A. 18 B. 14 C. 13 D. 8 |
C |
| 48. |
Find the median score A. 14.5 B. 14.0 C. 13.5 D. 13.0 Detailed Solution\(\frac{13 + 14}{2}\) = 13.5 |
|
| 49. |
How many students scored above the mean score? A. 10 B. 9 C. 8 D. 7 Detailed SolutionMean = 13.4No above mean is 7 |
|
| 50. |
Evaluate: \(\frac{0.42 + 2.5}{0.5 \times 2.95}\), leaving the answer in the standard form. A. 1.639 x 10\(^2\) B. 1.639 x 10\(^1\) C. 1.639 x 10\(^{-1}\) D. 1.639 x 10\(^{-2}\) Detailed Solution\(\frac{0.42 \div 2.5}{0.5 \times 2.05} = \frac{0.168}{1.025}\)= 1.639 x 10\(^{-1}\) |
