Year :
2019
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
21 - 30 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
The total surface area of a solid cylinder 165cm\(^2\). Of the base diameter is 7cm, calculate its height. [Take \(\pi = \frac{22}{7}\)] A. 7.5 cm B. 4.5 cm C. 4.0 cm D. 2.0 cm Detailed Solution165 = 2 x \(\frac{22}{7}\) x \(\frac{7}{2}\) x h + 2 x \(\frac{22}{7}\) x \(\frac{7}{2}\) x \(\frac{7}{2}\)165 = 22h + 77 \(\frac{22h}{22} = \frac{88}{22}\) height = 4cm |
|
| 22. |
If 2\(^{a}\) = \(\sqrt{64}\) and \(\frac{b}{a}\) = 3, evaluate a\(^2 + b^{2}\) A. 250 B. 160 C. 90 D. 48 Detailed Solution2\(^a\) = \(\sqrt{64}\)2\(^a\) = 8 2\(^a\) = 2\(^3\) a = 3 b = 3\(^a\) b = 3 x 3 = 9 a\(^2\) + b\(^2\) = 3\(^2\) + 9\(^2\) = 9 + 81 = 90 |
|
| 23. |
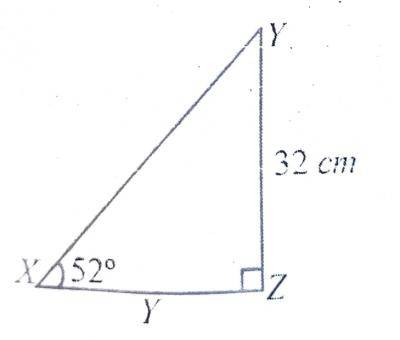 In XYZ, |YZ| = 32cm, < YXZ 53\(^o\) and XZY = 90\(^o\). Find, correct to the nearest centimetre, |XZ| A. 31 cm B. 25 cm C. 20 cm D. 13 cm Detailed SolutionTan 52\(^o\) = \(\frac{32}{\text{|XZ|}}\)|XZ| = \(\frac{32}{Tan 52^o}\) = 25cm |
|
| 24. |
If log\(_x\) 2 = 0.3, evaluate log\(_x\) 8. A. 2.4 B. 1.2 C. 0.9 D. 0.6 Detailed Solutionlog\(_x\)2 = 0.3log\(_x\)8 = log\(_x\)2\(^3\) = 3 log\(_x\)2 = 3 x 0.3 = 0.9 |
|
| 25. |
An arc subtends an angle of 72\(^o\) at the centre of a circle. Find the length of the arc if the radius of the circle is 3.5 cm. [Take \(\pi = \frac{22}{7}\)] A. 6.6 cm B. 8.8 cm C. 4.4 cm D. 2.2 cm Detailed SolutionLength = \(\frac{\theta}{360}\) x 2\(\pi\)r= \(\frac{72}{360} \times 2 \frac{22}{7} \times \frac{0.5}{3.5}\) = 4.4 |
|
| 26. |
Make b the subject of the relation lb = \(\frac{1}{2}\) (a + b)h A. \(\frac{ah}{2l - h}\) B. \(\frac{2l - h}{al}\) C. \(\frac{al}{2l - h}\) D. \(\frac{al}{2 - h}\) Detailed Solutionlb = \(\frac{1}{2} (a + b)h2lb = ah + bh 2lb - bh = ah \(\frac{b(2l - h)}{2l - h} = \frac{ah}{2l - h}\) b = \(\frac{ah}{2l - h}\) |
|
| 27. |
Eric sold his house through an agent who charged 8% commission on the selling price. If Eric received $117,760.00 after the sale, what was the selling price of the house? A. $130,000.00 B. $128,000.00 C. $125,000.00 D. $120,000.00 Detailed Solution\(\frac{8}{100} \times x + 117,760 = x\)x - \(\frac{8x}{100} = 117,760 \(\frac{92x}{100} = 117,760\) x = \(\frac{117,760 \times 100}{92}\) Selling price = N128,000 |
|
| 28. |
Find the angle at which an arc of length 22 cm subtends at the centre of a circle of radius 15cm. [Take \(\pi = \frac{22}{7}\)] A. 70\(^o\) B. 84\(^o\) C. 96\(^o\) D. 156\(^o\) Detailed SolutionL = \(\frac{\theta}{360} \times 2 \pi r\)22 = \(\frac{theta}{360} \times 2 \times \frac{22}{7} \times 15\) \(\theta = \frac{22 \times 360 \times 7}{2 \times 22 \times 15}\) \(\theta\) = 84\(^o\) |
|
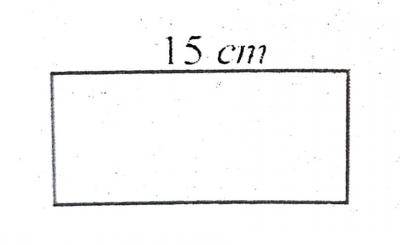
| 29. |
A rectangular board has a length of 15cm and width x cm. If its sides are doubled, find its new area. A. 60x cm\(^2\) B. 45x cm\(^2\) C. 30x cm\(^2\) D. 15x cm\(^2\) Detailed Solution
= 60cm\(^2\) |
|
| 30. |
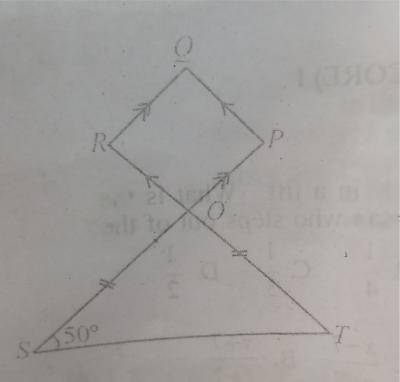 In the diagram, POS and ROT re straight lines. OPOR is a parallelogram, |OS| = |OT| and |QR| = |QP|. Find angle O. A. 100\(^o\) B. 120\(^o\) C. 140\(^o\) D. 160\(^o\) Detailed SolutionS\(O\)T = 180\(^o\) - (50 + 50)= 80\(^o\) P\(Q\)R = 80\(^o\) = \(\frac{360^o - 160^o}{2}\) = 100\(^o\) |
| 21. |
The total surface area of a solid cylinder 165cm\(^2\). Of the base diameter is 7cm, calculate its height. [Take \(\pi = \frac{22}{7}\)] A. 7.5 cm B. 4.5 cm C. 4.0 cm D. 2.0 cm Detailed Solution165 = 2 x \(\frac{22}{7}\) x \(\frac{7}{2}\) x h + 2 x \(\frac{22}{7}\) x \(\frac{7}{2}\) x \(\frac{7}{2}\)165 = 22h + 77 \(\frac{22h}{22} = \frac{88}{22}\) height = 4cm |
|
| 22. |
If 2\(^{a}\) = \(\sqrt{64}\) and \(\frac{b}{a}\) = 3, evaluate a\(^2 + b^{2}\) A. 250 B. 160 C. 90 D. 48 Detailed Solution2\(^a\) = \(\sqrt{64}\)2\(^a\) = 8 2\(^a\) = 2\(^3\) a = 3 b = 3\(^a\) b = 3 x 3 = 9 a\(^2\) + b\(^2\) = 3\(^2\) + 9\(^2\) = 9 + 81 = 90 |
|
| 23. |
 In XYZ, |YZ| = 32cm, < YXZ 53\(^o\) and XZY = 90\(^o\). Find, correct to the nearest centimetre, |XZ| A. 31 cm B. 25 cm C. 20 cm D. 13 cm Detailed SolutionTan 52\(^o\) = \(\frac{32}{\text{|XZ|}}\)|XZ| = \(\frac{32}{Tan 52^o}\) = 25cm |
|
| 24. |
If log\(_x\) 2 = 0.3, evaluate log\(_x\) 8. A. 2.4 B. 1.2 C. 0.9 D. 0.6 Detailed Solutionlog\(_x\)2 = 0.3log\(_x\)8 = log\(_x\)2\(^3\) = 3 log\(_x\)2 = 3 x 0.3 = 0.9 |
|
| 25. |
An arc subtends an angle of 72\(^o\) at the centre of a circle. Find the length of the arc if the radius of the circle is 3.5 cm. [Take \(\pi = \frac{22}{7}\)] A. 6.6 cm B. 8.8 cm C. 4.4 cm D. 2.2 cm Detailed SolutionLength = \(\frac{\theta}{360}\) x 2\(\pi\)r= \(\frac{72}{360} \times 2 \frac{22}{7} \times \frac{0.5}{3.5}\) = 4.4 |
| 26. |
Make b the subject of the relation lb = \(\frac{1}{2}\) (a + b)h A. \(\frac{ah}{2l - h}\) B. \(\frac{2l - h}{al}\) C. \(\frac{al}{2l - h}\) D. \(\frac{al}{2 - h}\) Detailed Solutionlb = \(\frac{1}{2} (a + b)h2lb = ah + bh 2lb - bh = ah \(\frac{b(2l - h)}{2l - h} = \frac{ah}{2l - h}\) b = \(\frac{ah}{2l - h}\) |
|
| 27. |
Eric sold his house through an agent who charged 8% commission on the selling price. If Eric received $117,760.00 after the sale, what was the selling price of the house? A. $130,000.00 B. $128,000.00 C. $125,000.00 D. $120,000.00 Detailed Solution\(\frac{8}{100} \times x + 117,760 = x\)x - \(\frac{8x}{100} = 117,760 \(\frac{92x}{100} = 117,760\) x = \(\frac{117,760 \times 100}{92}\) Selling price = N128,000 |
|
| 28. |
Find the angle at which an arc of length 22 cm subtends at the centre of a circle of radius 15cm. [Take \(\pi = \frac{22}{7}\)] A. 70\(^o\) B. 84\(^o\) C. 96\(^o\) D. 156\(^o\) Detailed SolutionL = \(\frac{\theta}{360} \times 2 \pi r\)22 = \(\frac{theta}{360} \times 2 \times \frac{22}{7} \times 15\) \(\theta = \frac{22 \times 360 \times 7}{2 \times 22 \times 15}\) \(\theta\) = 84\(^o\) |
|
| 29. |
A rectangular board has a length of 15cm and width x cm. If its sides are doubled, find its new area. A. 60x cm\(^2\) B. 45x cm\(^2\) C. 30x cm\(^2\) D. 15x cm\(^2\) Detailed Solution
= 60cm\(^2\) |
|
| 30. |
 In the diagram, POS and ROT re straight lines. OPOR is a parallelogram, |OS| = |OT| and |QR| = |QP|. Find angle O. A. 100\(^o\) B. 120\(^o\) C. 140\(^o\) D. 160\(^o\) Detailed SolutionS\(O\)T = 180\(^o\) - (50 + 50)= 80\(^o\) P\(Q\)R = 80\(^o\) = \(\frac{360^o - 160^o}{2}\) = 100\(^o\) |