Year :
2019
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
Factorize completely; (2x + 2y)(x - y) + (2x - 2y)(x + y) A. 4(x - y)(x + y) B. (4(x - y) C. 2(x - y)(x + y) D. 2(x - y) Detailed Solution(2x + 2y)(x - y) + (2x - 2y)(x - y)2(x + y)(x - y) + 2(x - y)(x + y) 4(x - y)(x + y) |
|
| 32. |
The interior angles of a polygon are 3x\(^o\), 2x\(^o\), 4x\(^o\), 3x\(^o\) and 6\(^o\). Find the size of the smallest angle of the polygon. A. 80\(^o\) B. 60\(^o\) C. 40\(^o\) D. 30\(^o\) Detailed Solution3\(x^o\) + 2\(x^o\) + 4\(x^o\) + 3\(x^o\) + 6\(x^o\) = 540\(x^o\)\(\frac{18x^o}{18} = \frac{540^o}{18}\) \(x^o\) = 30\(^o\) Smallest angle = 2 x 30\(^o\) = 60\(^o\) |
|
| 33. |
A box contains 3 white and 3 blue identical balls. If two balls are picked at random from the box, one after the other with replacement, what is the probability that they are of different colours? A. \(\frac{2}{3}\) B. \(\frac{3}{5}\) C. \(\frac{7}{20}\) D. \(\frac{12}{25}\) Detailed Solution(\(\frac{2}{5} \times \frac {3}{5}) + (\frac{3}{5} \times \frac{2}{5})\)\(\frac{6}{25} + \frac{6}{25} = \frac{12}{25}\) |
|
| 34. |
Find the equation of a straight line passing through the point (1, -5) and having gradient of \(\frac{3}{4}\) A. 3x + 4y - 23 = 0 B. 3x + 4y +23 = 0 C. 3x - 4y +23 = 0 D. 3x - 4y - 23 = 0 Detailed Solution\(\frac{3}{4} = \frac{y + 5}{x - 1}\)3(x - 1) = 4(y + 5) 3x - 3 = 4y + 20 3x - 4y - 23 = 0 |
|
| 35. |
The foot of a ladder is 6m from the base of an electric pole. The top of the ladder rest against the pole at a point 8m above the ground. How long is the ladder? A. 14m B. 12m C. 10m D. 7m Detailed SolutionH\(^2\) = 8\(^2\) + 6\(^2\) + 6\(^2\)H\(^2\) = 64 + 36 = 100 H = \(\sqrt{100}\) = 10m |
|
| 36. |
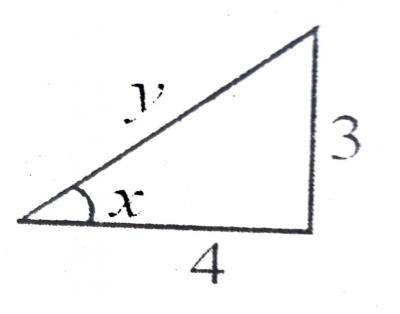
If tan x = \(\frac{3}{4}\), 0 < x < 90\(^o\), evaluate \(\frac{\cos x}{2 sin x}\) A. \(\frac{8}{3}\) B. \(\frac{3}{2}\) C. \(\frac{4}{3}\) D. \(\frac{2}{3}\) Detailed Solution
y\(^2\) = 9 + 16 y = \(\sqrt{25}\) = 5 \(\frac{\cos x}{2 \sin x} = \frac{4}{5} + 2 \times \frac{3}{5}\) = \(\frac{4}{5} \times \frac{5}{6}\) = \(\frac{2}{3}\) |
|
| 37. |
From the top of a vehicle cliff 20m high, a boat at sea can be sighted 75m away and on the same horizontal position as the cliff. Calculate, correct to the nearest degree, the angle of depression of the boat from the top of the cliff. A. 56\(^o\) B. 75\(^o\) C. 16\(^o\) D. 15\(^o\) Detailed Solution
\(\theta = sin^{-1} (\frac{20}{75})\) = 15\(^o\) |
|
| 38. |
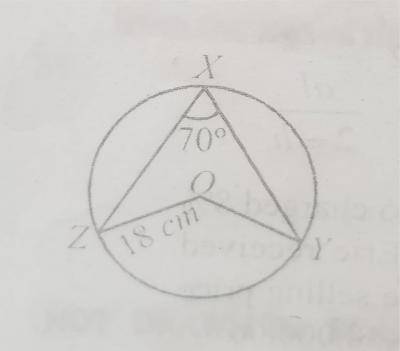 In the diagram, O is the centre of the circle of radius 18cm. If < zxy = 70\(^o\), calculate the length of arc ZY. [Take \(\pi = \frac{22}{7}\)] A. 11cm B. 22 cm C. 44 cm D. 80 cm Detailed SolutionZ\({O}\)T = 2 x 70\(^o\) 140\(^o\)Length = \(\frac{\theta}{360}\) x 2\(\pi\)r \(\frac{140^o}{360} \times 2 \times \frac{22}{7}\) x 18 = 44cm |
|
| 39. |
 In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Find the value of y. A. 70\(^o\) B. 60\(^o\) C. 52\(^o\) D. 18\(^o\) Detailed SolutionR\(P\)Q = R\(S\)Q = 52\(o\)y = 52\(^o\) |
|
| 40. |
 In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Calculate the value of x. A. 70\(^o\) B. 58\(^o\) C. 55\(^o\) D. 48\(^o\) Detailed Solutionx = 180\(^o\) - (52\(^o\) + 70\(^o\))= 180\(o\) - 122\(^o\) = 58\(^o\) |
| 31. |
Factorize completely; (2x + 2y)(x - y) + (2x - 2y)(x + y) A. 4(x - y)(x + y) B. (4(x - y) C. 2(x - y)(x + y) D. 2(x - y) Detailed Solution(2x + 2y)(x - y) + (2x - 2y)(x - y)2(x + y)(x - y) + 2(x - y)(x + y) 4(x - y)(x + y) |
|
| 32. |
The interior angles of a polygon are 3x\(^o\), 2x\(^o\), 4x\(^o\), 3x\(^o\) and 6\(^o\). Find the size of the smallest angle of the polygon. A. 80\(^o\) B. 60\(^o\) C. 40\(^o\) D. 30\(^o\) Detailed Solution3\(x^o\) + 2\(x^o\) + 4\(x^o\) + 3\(x^o\) + 6\(x^o\) = 540\(x^o\)\(\frac{18x^o}{18} = \frac{540^o}{18}\) \(x^o\) = 30\(^o\) Smallest angle = 2 x 30\(^o\) = 60\(^o\) |
|
| 33. |
A box contains 3 white and 3 blue identical balls. If two balls are picked at random from the box, one after the other with replacement, what is the probability that they are of different colours? A. \(\frac{2}{3}\) B. \(\frac{3}{5}\) C. \(\frac{7}{20}\) D. \(\frac{12}{25}\) Detailed Solution(\(\frac{2}{5} \times \frac {3}{5}) + (\frac{3}{5} \times \frac{2}{5})\)\(\frac{6}{25} + \frac{6}{25} = \frac{12}{25}\) |
|
| 34. |
Find the equation of a straight line passing through the point (1, -5) and having gradient of \(\frac{3}{4}\) A. 3x + 4y - 23 = 0 B. 3x + 4y +23 = 0 C. 3x - 4y +23 = 0 D. 3x - 4y - 23 = 0 Detailed Solution\(\frac{3}{4} = \frac{y + 5}{x - 1}\)3(x - 1) = 4(y + 5) 3x - 3 = 4y + 20 3x - 4y - 23 = 0 |
|
| 35. |
The foot of a ladder is 6m from the base of an electric pole. The top of the ladder rest against the pole at a point 8m above the ground. How long is the ladder? A. 14m B. 12m C. 10m D. 7m Detailed SolutionH\(^2\) = 8\(^2\) + 6\(^2\) + 6\(^2\)H\(^2\) = 64 + 36 = 100 H = \(\sqrt{100}\) = 10m |
| 36. |
If tan x = \(\frac{3}{4}\), 0 < x < 90\(^o\), evaluate \(\frac{\cos x}{2 sin x}\) A. \(\frac{8}{3}\) B. \(\frac{3}{2}\) C. \(\frac{4}{3}\) D. \(\frac{2}{3}\) Detailed Solution
y\(^2\) = 9 + 16 y = \(\sqrt{25}\) = 5 \(\frac{\cos x}{2 \sin x} = \frac{4}{5} + 2 \times \frac{3}{5}\) = \(\frac{4}{5} \times \frac{5}{6}\) = \(\frac{2}{3}\) |
|
| 37. |
From the top of a vehicle cliff 20m high, a boat at sea can be sighted 75m away and on the same horizontal position as the cliff. Calculate, correct to the nearest degree, the angle of depression of the boat from the top of the cliff. A. 56\(^o\) B. 75\(^o\) C. 16\(^o\) D. 15\(^o\) Detailed Solution
\(\theta = sin^{-1} (\frac{20}{75})\) = 15\(^o\) |
|
| 38. |
 In the diagram, O is the centre of the circle of radius 18cm. If < zxy = 70\(^o\), calculate the length of arc ZY. [Take \(\pi = \frac{22}{7}\)] A. 11cm B. 22 cm C. 44 cm D. 80 cm Detailed SolutionZ\({O}\)T = 2 x 70\(^o\) 140\(^o\)Length = \(\frac{\theta}{360}\) x 2\(\pi\)r \(\frac{140^o}{360} \times 2 \times \frac{22}{7}\) x 18 = 44cm |
|
| 39. |
 In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Find the value of y. A. 70\(^o\) B. 60\(^o\) C. 52\(^o\) D. 18\(^o\) Detailed SolutionR\(P\)Q = R\(S\)Q = 52\(o\)y = 52\(^o\) |
|
| 40. |
 In the diagram, RT is a tangent to the circle at R, < PQR = 70\(^o\), < QRT = 52\(^o\), < QSR and < PRQ = x. Calculate the value of x. A. 70\(^o\) B. 58\(^o\) C. 55\(^o\) D. 48\(^o\) Detailed Solutionx = 180\(^o\) - (52\(^o\) + 70\(^o\))= 180\(o\) - 122\(^o\) = 58\(^o\) |