Year : 
1992
Title : 
Mathematics (Core)
Exam : 
JAMB Exam

Paper 1 | Objectives

21 - 30 of 49 Questions

# Question Ans
21.

P = \(\begin{vmatrix} x & 3 & 0 \\ 2 & y & 3\\ 4 & 2 & 4 \end{vmatrix}\)

Q = \(\begin{vmatrix} x & 2 & z \\ 3 & y & 2\\ 0 & 3 & z \end{vmatrix}\) Where pT is the transpose P calculate /pT/ when x = 0, y = 1 and z = 2

A. 48

B. 24

C. -24

D. -48

Detailed Solution

p = \(\begin{vmatrix} 0 & 3 & 0 \\ 2 & 1 & 3\\ 4 & 2 & 2 \end{vmatrix}\)

PT = \(\begin{vmatrix}0 & 2 & 4 \\ 2 & 1 & 3\\ 0 & 3 & 2 \end{vmatrix}\)

/pT/ = \(\begin{vmatrix}0 & 2 & 4 \\ 3 & 1 & 3\\ 0 & 3 & 2 \end{vmatrix}\)

= 0[2 - 6] - 2[6 - 0] + 4[9 - 0]

= 0 - 12 + 36 = 24
22.

P = \(\begin{vmatrix} x & 3 & 0 \\ 2 & y & 3\\ 4 & 2 & 4 \end{vmatrix}\)

Q = \(\begin{vmatrix} x & 2 & z \\ 3 & y & 2\\ 0 & 3 & z \end{vmatrix}\)
PQ is equivalent to

A. PPT

B. pp-1

C. qp

D. pp

Detailed Solution

p = \(\begin{vmatrix} 0 & 3 & 0 \\ 2 & 1 & 3\\ 4 & 2 & 2 \end{vmatrix}\)

Q = \(\begin{vmatrix} 0 & 2 & 4 \\ 3 & 1 & 2\\ 0 & 3 & 2 \end{vmatrix}\) = pT

pq = ppT
23.

If the angles of quadrilateral are (p + 10)°, (2p - 30)°, (3p + 20)° and 4p°, find p.

A. 63

B. 40

C. 36

D. 28

Detailed Solution

The sum of angles in a quadrilateral = 360°
\(\therefore (p + 10) + (2p - 30) + (3p + 20) + 4p = 360\)
\(10p = 360° \implies p = \frac{360}{10} = 36°\)
24.

Determine the distance on the earth's surface between two town P (lat 60°N, Long 20°E) and Q(Lat 60°N, Long 25°W) (Radius of the earth = 6400km)

A. \(\frac{800\pi}{9}\)km

B. \(\frac{800\sqrt{3\pi}}{9}\)km

C. 800\(\pi\) km

D. 800\(\sqrt{3\pi}\) km

Detailed Solution

Angular difference (\(\theta\))= 25° + 20° = 45°
\(\alpha\) = common latitude = 60°
\(S = \frac{\theta}{360°} \times 2\pi R \cos \alpha\)
\(S = \frac{45°}{360°} \times 2 \pi \times 6400 \times \cos 60°\)
= \(\frac{6400\pi}{8} = 800\pi km\)
25.

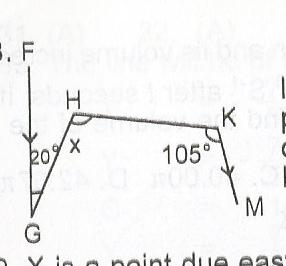If in the diagram, FG is parallel to KM, find the value of x

A. 75o

B. 95o

C. 105o

D. 125o

B
26.

X is a point due east of point Y on a coast: Z is another point on the coast but 6√3km due south of y.If the distance XZ is 12Km. Calculate the bearing of Z from X

A. 240o

B. 210o

C. 150o

D. 60o

Detailed Solution

Using sinØ = \(\frac{6√3}{12}\) → \(\frac{√3}{2}\)
sinØ = \(\frac{√3}{2}\) or 60°
The bearing of Z from X = [270 - 60]° → 210°
27.

The locus of a point which is equidistant from two given fixed points is the

A. perpendicular bisector of the straight line joining them

B. parallel line to the straight line joining them

C. transverse to the straight line joining them

D. angle bisector of 90o which the straight line joining them makes with the horizontal

A
28.

What is the perpendicular distance of a point (2, 3) from the line 2x - 4y + 3 = 0?

A. \(\frac{\sqrt{5}}{2}\)

B. \(\frac{\sqrt{5}}{20}\)

C. \(\frac{5}{\sqrt{13}}\)

D. 6

Detailed Solution

2x - 4y + 3 = 0

Required distance = \(\frac{(2 \times 2) + 3(-4) + 3}{\sqrt{2^2} + (-4)^2}\)

= \(\frac{4 - 12 + 3}{\sqrt{20}}\)

= \(\frac{-5}{-2\sqrt{5}}\)

= \(\frac{\sqrt{5}}{2}\)
29.

Find then equation line through (5, 7) parallel to the line 7x + 5y = 12

A. 5x + 7y = 120

B. 7x + 5y = 70

C. x + y = 7

D. 15x + 17y = 90

Detailed Solution

Equation (5, 7) parallel to the line 7x + 5y = 12

5Y = -7x + 12

y = \(\frac{-7x}{5}\) + \(\frac{12}{5}\)

Gradient = \(\frac{-7}{5}\)

∴ Required equation = \(\frac{y - 7}{x - 5}\) = \(\frac{-7}{5}\) i.e. 5y - 35 = -7x + 35

5y + 7x = 70
30.

Given that \(\theta\) is an acute angle and sin \(\theta\) = \(\frac{m}{n}\), find cos \(\theta\)

A. \(\frac{\sqrt{n^2 - m^2}}{m}\)

B. \(\frac{\sqrt{(n + m)(n - m)}}{n}\)

C. \(\frac{m}{\sqrt{n^2 - m^2}}\)

D. \(\sqrt{\frac{n}{n^2 - m^2}}\)

Detailed Solution

sin \(\theta\) = \(\frac{m}{n}\)
Opp = m; Hyp = n
Adj = \(\sqrt{n^{2} - m^{2}}\)
\(\cos \theta = \frac{\sqrt{n^{2} - m^{2}}}{n}\)
= \(\frac{\sqrt{(n + m)(n - m)}}{n}\)
21.

P = \(\begin{vmatrix} x & 3 & 0 \\ 2 & y & 3\\ 4 & 2 & 4 \end{vmatrix}\)

Q = \(\begin{vmatrix} x & 2 & z \\ 3 & y & 2\\ 0 & 3 & z \end{vmatrix}\) Where pT is the transpose P calculate /pT/ when x = 0, y = 1 and z = 2

A. 48

B. 24

C. -24

D. -48

Detailed Solution

p = \(\begin{vmatrix} 0 & 3 & 0 \\ 2 & 1 & 3\\ 4 & 2 & 2 \end{vmatrix}\)

PT = \(\begin{vmatrix}0 & 2 & 4 \\ 2 & 1 & 3\\ 0 & 3 & 2 \end{vmatrix}\)

/pT/ = \(\begin{vmatrix}0 & 2 & 4 \\ 3 & 1 & 3\\ 0 & 3 & 2 \end{vmatrix}\)

= 0[2 - 6] - 2[6 - 0] + 4[9 - 0]

= 0 - 12 + 36 = 24
22.

P = \(\begin{vmatrix} x & 3 & 0 \\ 2 & y & 3\\ 4 & 2 & 4 \end{vmatrix}\)

Q = \(\begin{vmatrix} x & 2 & z \\ 3 & y & 2\\ 0 & 3 & z \end{vmatrix}\)
PQ is equivalent to

A. PPT

B. pp-1

C. qp

D. pp

Detailed Solution

p = \(\begin{vmatrix} 0 & 3 & 0 \\ 2 & 1 & 3\\ 4 & 2 & 2 \end{vmatrix}\)

Q = \(\begin{vmatrix} 0 & 2 & 4 \\ 3 & 1 & 2\\ 0 & 3 & 2 \end{vmatrix}\) = pT

pq = ppT
23.

If the angles of quadrilateral are (p + 10)°, (2p - 30)°, (3p + 20)° and 4p°, find p.

A. 63

B. 40

C. 36

D. 28

Detailed Solution

The sum of angles in a quadrilateral = 360°
\(\therefore (p + 10) + (2p - 30) + (3p + 20) + 4p = 360\)
\(10p = 360° \implies p = \frac{360}{10} = 36°\)
24.

Determine the distance on the earth's surface between two town P (lat 60°N, Long 20°E) and Q(Lat 60°N, Long 25°W) (Radius of the earth = 6400km)

A. \(\frac{800\pi}{9}\)km

B. \(\frac{800\sqrt{3\pi}}{9}\)km

C. 800\(\pi\) km

D. 800\(\sqrt{3\pi}\) km

Detailed Solution

Angular difference (\(\theta\))= 25° + 20° = 45°
\(\alpha\) = common latitude = 60°
\(S = \frac{\theta}{360°} \times 2\pi R \cos \alpha\)
\(S = \frac{45°}{360°} \times 2 \pi \times 6400 \times \cos 60°\)
= \(\frac{6400\pi}{8} = 800\pi km\)
25.

If in the diagram, FG is parallel to KM, find the value of x

A. 75o

B. 95o

C. 105o

D. 125o

B
26.

X is a point due east of point Y on a coast: Z is another point on the coast but 6√3km due south of y.If the distance XZ is 12Km. Calculate the bearing of Z from X

A. 240o

B. 210o

C. 150o

D. 60o

Detailed Solution

Using sinØ = \(\frac{6√3}{12}\) → \(\frac{√3}{2}\)
sinØ = \(\frac{√3}{2}\) or 60°
The bearing of Z from X = [270 - 60]° → 210°
27.

The locus of a point which is equidistant from two given fixed points is the

A. perpendicular bisector of the straight line joining them

B. parallel line to the straight line joining them

C. transverse to the straight line joining them

D. angle bisector of 90o which the straight line joining them makes with the horizontal

A
28.

What is the perpendicular distance of a point (2, 3) from the line 2x - 4y + 3 = 0?

A. \(\frac{\sqrt{5}}{2}\)

B. \(\frac{\sqrt{5}}{20}\)

C. \(\frac{5}{\sqrt{13}}\)

D. 6

Detailed Solution

2x - 4y + 3 = 0

Required distance = \(\frac{(2 \times 2) + 3(-4) + 3}{\sqrt{2^2} + (-4)^2}\)

= \(\frac{4 - 12 + 3}{\sqrt{20}}\)

= \(\frac{-5}{-2\sqrt{5}}\)

= \(\frac{\sqrt{5}}{2}\)
29.

Find then equation line through (5, 7) parallel to the line 7x + 5y = 12

A. 5x + 7y = 120

B. 7x + 5y = 70

C. x + y = 7

D. 15x + 17y = 90

Detailed Solution

Equation (5, 7) parallel to the line 7x + 5y = 12

5Y = -7x + 12

y = \(\frac{-7x}{5}\) + \(\frac{12}{5}\)

Gradient = \(\frac{-7}{5}\)

∴ Required equation = \(\frac{y - 7}{x - 5}\) = \(\frac{-7}{5}\) i.e. 5y - 35 = -7x + 35

5y + 7x = 70
30.

Given that \(\theta\) is an acute angle and sin \(\theta\) = \(\frac{m}{n}\), find cos \(\theta\)

A. \(\frac{\sqrt{n^2 - m^2}}{m}\)

B. \(\frac{\sqrt{(n + m)(n - m)}}{n}\)

C. \(\frac{m}{\sqrt{n^2 - m^2}}\)

D. \(\sqrt{\frac{n}{n^2 - m^2}}\)

Detailed Solution

sin \(\theta\) = \(\frac{m}{n}\)
Opp = m; Hyp = n
Adj = \(\sqrt{n^{2} - m^{2}}\)
\(\cos \theta = \frac{\sqrt{n^{2} - m^{2}}}{n}\)
= \(\frac{\sqrt{(n + m)(n - m)}}{n}\)