Mathematics (Core), 1991, WASSCE/WAEC MAY/JUNE, Exam, Paper 1 | Objectives

Paper Info

Year :

1991

Title :

Mathematics (Core)

Exam :

WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

41 - 50 of 50 Questions

#	Question	Ans
41.	Mrs. Jones is expecting a baby. The probability that it will be a boy is 1/2 and probability that the baby will have blue eyes is 1/4. What is the probability that she will have a blue-eyed boy? A. 1/8 B. ¹/₄ C. 3/8 D. ¹/₂ E. 3/4 Show Content Detailed Solution (1/2)(1/4) = 1/8	A
42.	Which of the following about a rhombus may not be true? A. The diagonals are equal B. The diagonals bisect the angles through which they pass C. the diagonals bisect each other D. The adjacent sides are equal E. Opposite angles are equal	A
43.	The angles of a pentagon are x°, 2x°, (x + 60)°, (x + 10)°, (x -10)°. Find the value of x. A. 40 B. 60 C. 75 D. 80 E. 90 Show Content Detailed Solution Sum of ∠s in a pentagon = (n - 2)180 = 540° x° + 2x° + x° + 60° + x° + 10° + x° - 10° = 540° 6x° + 60° = 540°; x = 80°	D
44.	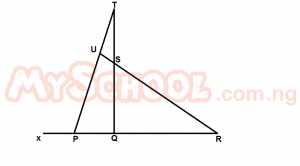In the diagram above, ∠PTQ = ∠URP = 25° and XPU = 4URP. Calculate ∠USQ. A. 100^o B. 120^o C. 125^o D. 130^o E. 150^o Show Content Detailed Solution Since < URP = 25°, then < XPU = 4 x 25° = 100° \(\therefore\) < TPQ = 180° - 100° = 80° \(\therefore\) < PQT = 180° - (80° + 25°) = 75° < SQR = 75° - 25° = 50° (exterior angle = 2 opp interior angles) \(\therefore\) < USQ = 180° - 50° = 130°	D
45.	In a given regular polygon, the ratio of the exterior angle to the interior angles is 1:3. How many side has the polygon? A. 40 B. 5 C. 6 D. 8 E. 12 Show Content Detailed Solution Let x be the exterior angle; interior = 3x; but x + 3x = 180^o 4x = 180^o; x = 45 = \(\frac{360}{45}\) = 8	D
46.	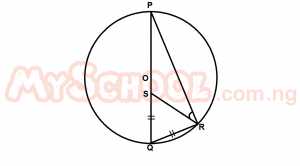In the diagram above, O is the center of the circle, \|SQ\| = \|QR\| and ∠PQR = 68°. Calculate ∠PRS A. 34^o B. 45^o C. 56^o D. 62^o E. 68^o Show Content Detailed Solution From the figure, < PQR = 68° \(\therefore\) < QRS = < QSR = \(\frac{180 - 68}{2}\) (base angles of an isos. triangle) = 56° \(\therefore\) < PRS = 90° - 56° = 34° (angles in a semi-circle)	A
47.	Find the area of an equivalent triangle of side 16cm A. 64√3cm² B. 72√3cm² C. 96cm² D. 128√3cm² E. 128cm² Show Content Detailed Solution Area = ¹/₂ x 16 x 16sin60^o = 64√3cm²	A
48.	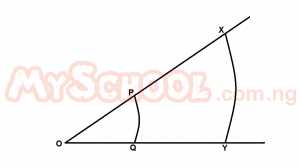In the diagram above, PQ and XY are two concentric arc; center O, the ratio of the length of the two arc is 1:3, find the ratio of the areas of the two sectors OPQ and OXY A. 1:3 B. 1:6 C. 1:9 D. 2:3 E. 4:9 Show Content Detailed Solution Let the radius of the arc PQ = r and the radius of the arc XY = R. Length of arc PQ = \(\frac{\theta}{360} \times 2\pi r = 1\) Length of arc XY = \(\frac{\theta}{360} \times 2\pi R = 3\) Ratio of the arc = \(\frac{r}{R} = \frac{360 \times 2\pi \theta}{2\pi \theta \times 360 \times 3}\) = \(\frac{1}{3}\) Ratio of their area = \((\frac{1}{3})^2 = \frac{1}{9}\) = 1 : 9	C
49.	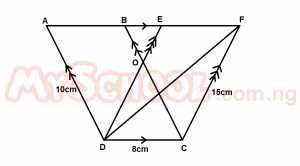In the diagram above , \|AD\| = 10cm, \|DC\| = 8cm and \|CF\| = 15cmIf the area of triangle DCF = 24cm², find the area of the quadrilateral ABCD. A. 24cm² B. 48cm² C. 80cm² D. 96cm² E. 120cm² Show Content Detailed Solution Area of \(\Delta\)DCF = 24cm² Area of Quad= 2 x 24 = 48cm²	B
50.	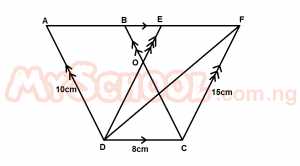In the diagram above , \|AD\| = 10cm, \|DC\| = 8cm and \|CF\| = 15cm. Which of the following is correct? A. Area BCF = Area DCF B. Area ADE = Area ADF C. Area ADE = Area DCFE D. Area CBF = Area DABC E. Area DABO = Area CFEO	E

41.	Mrs. Jones is expecting a baby. The probability that it will be a boy is 1/2 and probability that the baby will have blue eyes is 1/4. What is the probability that she will have a blue-eyed boy? A. 1/8 B. ¹/₄ C. 3/8 D. ¹/₂ E. 3/4 Show Content Detailed Solution (1/2)(1/4) = 1/8	A
42.	Which of the following about a rhombus may not be true? A. The diagonals are equal B. The diagonals bisect the angles through which they pass C. the diagonals bisect each other D. The adjacent sides are equal E. Opposite angles are equal	A
43.	The angles of a pentagon are x°, 2x°, (x + 60)°, (x + 10)°, (x -10)°. Find the value of x. A. 40 B. 60 C. 75 D. 80 E. 90 Show Content Detailed Solution Sum of ∠s in a pentagon = (n - 2)180 = 540° x° + 2x° + x° + 60° + x° + 10° + x° - 10° = 540° 6x° + 60° = 540°; x = 80°	D
44.	In the diagram above, ∠PTQ = ∠URP = 25° and XPU = 4URP. Calculate ∠USQ. A. 100^o B. 120^o C. 125^o D. 130^o E. 150^o Show Content Detailed Solution Since < URP = 25°, then < XPU = 4 x 25° = 100° \(\therefore\) < TPQ = 180° - 100° = 80° \(\therefore\) < PQT = 180° - (80° + 25°) = 75° < SQR = 75° - 25° = 50° (exterior angle = 2 opp interior angles) \(\therefore\) < USQ = 180° - 50° = 130°	D
45.	In a given regular polygon, the ratio of the exterior angle to the interior angles is 1:3. How many side has the polygon? A. 40 B. 5 C. 6 D. 8 E. 12 Show Content Detailed Solution Let x be the exterior angle; interior = 3x; but x + 3x = 180^o 4x = 180^o; x = 45 = \(\frac{360}{45}\) = 8	D

46.	In the diagram above, O is the center of the circle, \|SQ\| = \|QR\| and ∠PQR = 68°. Calculate ∠PRS A. 34^o B. 45^o C. 56^o D. 62^o E. 68^o Show Content Detailed Solution From the figure, < PQR = 68° \(\therefore\) < QRS = < QSR = \(\frac{180 - 68}{2}\) (base angles of an isos. triangle) = 56° \(\therefore\) < PRS = 90° - 56° = 34° (angles in a semi-circle)	A
47.	Find the area of an equivalent triangle of side 16cm A. 64√3cm² B. 72√3cm² C. 96cm² D. 128√3cm² E. 128cm² Show Content Detailed Solution Area = ¹/₂ x 16 x 16sin60^o = 64√3cm²	A
48.	In the diagram above, PQ and XY are two concentric arc; center O, the ratio of the length of the two arc is 1:3, find the ratio of the areas of the two sectors OPQ and OXY A. 1:3 B. 1:6 C. 1:9 D. 2:3 E. 4:9 Show Content Detailed Solution Let the radius of the arc PQ = r and the radius of the arc XY = R. Length of arc PQ = \(\frac{\theta}{360} \times 2\pi r = 1\) Length of arc XY = \(\frac{\theta}{360} \times 2\pi R = 3\) Ratio of the arc = \(\frac{r}{R} = \frac{360 \times 2\pi \theta}{2\pi \theta \times 360 \times 3}\) = \(\frac{1}{3}\) Ratio of their area = \((\frac{1}{3})^2 = \frac{1}{9}\) = 1 : 9	C
49.	In the diagram above , \|AD\| = 10cm, \|DC\| = 8cm and \|CF\| = 15cmIf the area of triangle DCF = 24cm², find the area of the quadrilateral ABCD. A. 24cm² B. 48cm² C. 80cm² D. 96cm² E. 120cm² Show Content Detailed Solution Area of \(\Delta\)DCF = 24cm² Area of Quad= 2 x 24 = 48cm²	B
50.	In the diagram above , \|AD\| = 10cm, \|DC\| = 8cm and \|CF\| = 15cm. Which of the following is correct? A. Area BCF = Area DCF B. Area ADE = Area ADF C. Area ADE = Area DCFE D. Area CBF = Area DABC E. Area DABO = Area CFEO	E