Year :
1991
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
11 - 20 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 11. |
Find the equation whose roots are -2/3 and -1/4 A. 12x2 + 11x + 2 = 0 B. 12x2 - 11x + 2 = 0 C. x2 - 11/12x + 2 = 0 D. 12x2 - 11x - 2 = 0 E. x2 - 11/12x - 2 = 0 Detailed Solutionx = \(-\frac{2}{3}\) and \(-\frac{1}{4}\)\(\implies (x + \frac{2}{3}) = 0; (x + \frac{1}{4}) = 0\) \((x + \frac{2}{3})(x + \frac{1}{4}) = 0\) \(x^{2} + \frac{1}{4}x + \frac{2}{3}x + \frac{1}{6} = 0\) \(x^2 + \frac{11}{12}x + \frac{1}{6} = 0\) \(12x^2 + 11x + 2 = 0\) |
|
| 12. |
Solve: 6(x - 4) + 3(x + 7) = 3 A. 3/2 B. 2/3 C. 1/2 D. 1/3 E. o Detailed Solution6(x - 4) + 3(x + 7) = 36x - 24 + 3x + 21 = 3 9x - 3 = 3 9x = 6 x = \(\frac{2}{3}\) |
|
| 13. |
If 2x + y = 7 and 3x - 2y = 3, by how much is 7x greater than 10? A. 1 B. 3 C. 7 D. 10 E. 17 Detailed Solution2x + y = 7 = i3x - 2y = 3 = ii i x 2 + ii = 4x + 2y = 14 \(\frac {3x - 2y = 3}{7x = 17}\) x = \(\frac {17}{7}\) = 7x = 17 x 1/7 x 7 17 - 10 = 7 |
|
| 14. |
A cylinder of base radius 4cm is open at one end . If the ratio of the area of its base to that of its curved surface is 1:4, calculate the height of the cylinder A. 1cm B. 2cm C. 4cm D. 8cm E. 16cm Detailed Solutionr= 4cm; base area = \(\pi\)r2; Curve S.A = 2\(\pi\)rh\(\frac{base area}{curved area}\) = 1/4; \(\pi\)/2\(\pi\)rh =h = \(\frac{4 x 4cm}{2}\) h= 8cm |
|
| 15. |
A headmaster contributes 7% of his income into a fund and his wife contributes 4% of her income. If the husband earns N5,500 per annum (p.a) and the wife earns N4,000 (P.a), find the sum of their annual contribution to the fund A. N1045 B. N605 C. N545 D. N490 E. N440 Detailed SolutionHusband contributions = \(\frac{7}{100}\) x N5,500 = N385Wife contribution = \(\frac{4}{100}\) x N4,000 = N160 Sum of their Annual contribution = N385 + N160 = N545 |
|
| 16. |
A car is travelling at an average speed of 80km/hr. Its speed in meters per second (m/s) is A. 13.3m/s B. 22.2m/s C. 133.3m/s D. 222.2m/s E. 1333.3m/s Detailed Solution80km/h = \(\frac{80}{60}\) x \(\frac{1000}{60}\) = 3 x 3= \(\frac{40 x 5}{9}\)= \(\frac{200m/s}{9}\) = 22.22m/s |
|
| 17. |
Mrs. Kofi sold an article for C7.50 instead of C12.75. Calculate her percentage of error, correct to one decimal place. A. 41.2% B. 18.3% C. 5.3% D. 1.7% E. 1.4% Detailed SolutionError =12.75 - 7.50 = 5.25Error % = \(\frac{5.25}{12.75}\) x 100% = 41.2% |
|
| 18. |
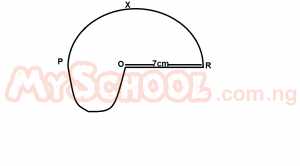 Find the area of the enclosed region, PXROY correct to the nearest whole number A. 96cm2 B. 116cm2 C. 154cm2 D. 192cm2 E. 385cm2 Detailed SolutionArea of the bigger semi circle P x RO =πr22 = 227 x 492 = 77cm2
|
|
| 19. |
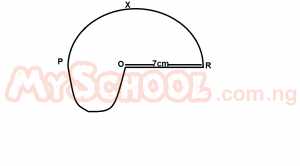 Find the perimeter of the region A. 22cm B. 33cm C. 40cm D. 47cm E. 66cm Detailed SolutionP = \(\pi\)r + \(\pi\)r + R = \(\frac{22}{7}\) x 7 + \(\frac{22}{7}\) x \(\frac{7}{2}\) + 7P = 22 + 11 + 7 = 40cm |
|
| 20. |
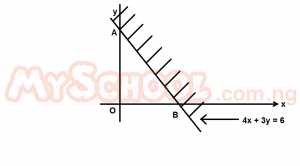 The shaded portion shows the outer boundary A. 4x + 3y \(\geq\) 6 B. 4x + 3y = 6 C. 4x + 3y < 6 D. 3y >6 E. 4x < 6 Detailed SolutionThe region is denoted by 4x + 3y \(\geq\) 6 |
| 11. |
Find the equation whose roots are -2/3 and -1/4 A. 12x2 + 11x + 2 = 0 B. 12x2 - 11x + 2 = 0 C. x2 - 11/12x + 2 = 0 D. 12x2 - 11x - 2 = 0 E. x2 - 11/12x - 2 = 0 Detailed Solutionx = \(-\frac{2}{3}\) and \(-\frac{1}{4}\)\(\implies (x + \frac{2}{3}) = 0; (x + \frac{1}{4}) = 0\) \((x + \frac{2}{3})(x + \frac{1}{4}) = 0\) \(x^{2} + \frac{1}{4}x + \frac{2}{3}x + \frac{1}{6} = 0\) \(x^2 + \frac{11}{12}x + \frac{1}{6} = 0\) \(12x^2 + 11x + 2 = 0\) |
|
| 12. |
Solve: 6(x - 4) + 3(x + 7) = 3 A. 3/2 B. 2/3 C. 1/2 D. 1/3 E. o Detailed Solution6(x - 4) + 3(x + 7) = 36x - 24 + 3x + 21 = 3 9x - 3 = 3 9x = 6 x = \(\frac{2}{3}\) |
|
| 13. |
If 2x + y = 7 and 3x - 2y = 3, by how much is 7x greater than 10? A. 1 B. 3 C. 7 D. 10 E. 17 Detailed Solution2x + y = 7 = i3x - 2y = 3 = ii i x 2 + ii = 4x + 2y = 14 \(\frac {3x - 2y = 3}{7x = 17}\) x = \(\frac {17}{7}\) = 7x = 17 x 1/7 x 7 17 - 10 = 7 |
|
| 14. |
A cylinder of base radius 4cm is open at one end . If the ratio of the area of its base to that of its curved surface is 1:4, calculate the height of the cylinder A. 1cm B. 2cm C. 4cm D. 8cm E. 16cm Detailed Solutionr= 4cm; base area = \(\pi\)r2; Curve S.A = 2\(\pi\)rh\(\frac{base area}{curved area}\) = 1/4; \(\pi\)/2\(\pi\)rh =h = \(\frac{4 x 4cm}{2}\) h= 8cm |
|
| 15. |
A headmaster contributes 7% of his income into a fund and his wife contributes 4% of her income. If the husband earns N5,500 per annum (p.a) and the wife earns N4,000 (P.a), find the sum of their annual contribution to the fund A. N1045 B. N605 C. N545 D. N490 E. N440 Detailed SolutionHusband contributions = \(\frac{7}{100}\) x N5,500 = N385Wife contribution = \(\frac{4}{100}\) x N4,000 = N160 Sum of their Annual contribution = N385 + N160 = N545 |
| 16. |
A car is travelling at an average speed of 80km/hr. Its speed in meters per second (m/s) is A. 13.3m/s B. 22.2m/s C. 133.3m/s D. 222.2m/s E. 1333.3m/s Detailed Solution80km/h = \(\frac{80}{60}\) x \(\frac{1000}{60}\) = 3 x 3= \(\frac{40 x 5}{9}\)= \(\frac{200m/s}{9}\) = 22.22m/s |
|
| 17. |
Mrs. Kofi sold an article for C7.50 instead of C12.75. Calculate her percentage of error, correct to one decimal place. A. 41.2% B. 18.3% C. 5.3% D. 1.7% E. 1.4% Detailed SolutionError =12.75 - 7.50 = 5.25Error % = \(\frac{5.25}{12.75}\) x 100% = 41.2% |
|
| 18. |
 Find the area of the enclosed region, PXROY correct to the nearest whole number A. 96cm2 B. 116cm2 C. 154cm2 D. 192cm2 E. 385cm2 Detailed SolutionArea of the bigger semi circle P x RO =πr22 = 227 x 492 = 77cm2
|
|
| 19. |
 Find the perimeter of the region A. 22cm B. 33cm C. 40cm D. 47cm E. 66cm Detailed SolutionP = \(\pi\)r + \(\pi\)r + R = \(\frac{22}{7}\) x 7 + \(\frac{22}{7}\) x \(\frac{7}{2}\) + 7P = 22 + 11 + 7 = 40cm |
|
| 20. |
 The shaded portion shows the outer boundary A. 4x + 3y \(\geq\) 6 B. 4x + 3y = 6 C. 4x + 3y < 6 D. 3y >6 E. 4x < 6 Detailed SolutionThe region is denoted by 4x + 3y \(\geq\) 6 |