Year :
2005
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 47 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
A train moving at a uniform speed covers 36km in 21 minutes. How long does it take to cover 60km? A. 35 mins B. 40 mins C. 45 mins D. 90 mins Detailed SolutionSince 36km in 21 minutes1km in \(\frac{21}{36}\)minutes 60km in \(\left(\frac{21}{36}\times 60\right)\)minutes = \(\frac{70}{2}\)min = 35 mins |
|
| 32. |
The salary of a man was increased in the ratio 40:47. calculate the percentage increase in the salary A. 85.1% B. 58.5% C. 17.5% D. 14.9% Detailed Solution\(\%Increase = \frac{Actual \hspace{1mm}increase}{initial \hspace{1mm}ratio}\times 100\%\)Actual increase = 7; Initial ratio = 40 \(=\left(\frac{7}{40} \times 100\%\right)=\frac{35}{2}=17.5\%\) |
|
| 33. |
A regular polygon has 9 sides. What is the size of one of its exterior angles? A. 20o B. 40o C. 90o D. 140o Detailed SolutionExterior angle \(=\frac{360}{n}\) where n = no of sides\(=\frac{360}{9}=40^{\circ}\) |
|
| 34. |
Simplify: \(\frac{2}{3xy} - \frac{3}{4yz}\) A. \(\frac{2-x}{12xyz}\) B. \(\frac{2z-3x}{12xyz}\) C. \(\frac{4z-3x}{12xyz}\) D. \(\frac{8z-9x}{12xyz}\) Detailed Solution\(\frac{2}{3xy} - \frac{3}{yz} = \frac{2(4)-3(3x)}{12xyz} = \frac{8z-9x}{12xyz}\) |
|
| 35. |
The total surface area of the walls of a room 7m long, 5m wide and xm high is 96m2. Find the value of x A. \(\frac{2}{3}\) B. 2 C. 4 D. 8 Detailed SolutionT.S.A of the wall \(=2(7\times 5 + 7 \times x + 5 \times x) = 96\\70 + 14x + 10x = 96 \Rightarrow 24x = 96-70=26\\ x = \frac{26}{24}=\frac{13}{12}\) |
|
| 36. |
For what values of y is the expression \(\frac{6y-1}{y^2 - y-6}\) A. \(\frac{1}{6}, \frac{1}{4}\) B. 3, -2 C. -3, 2 D. 0,1 Detailed SolutionThe expression is not defines when y2 - y - 6 = 0=> y2 - 3y + 2y - 6 = 0 => (y-3)(y+2) = 0 => y -3 = 0 or y + 2 = 0 => y = 3 or -2 |
|
| 37. |
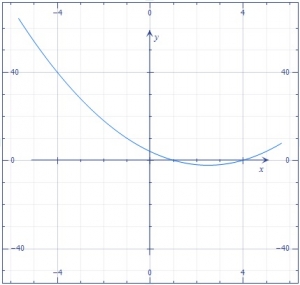 What are the roots of the equation? A. -1 and 1 B. 4 and 1 C. 1 and 4 D. 4 and 4 Detailed SolutionThe two points of contact of the curve with the x-axis are x = 1 and x = 4. The roots of the equation are x = 1 and x = 4 |
|
| 38. |
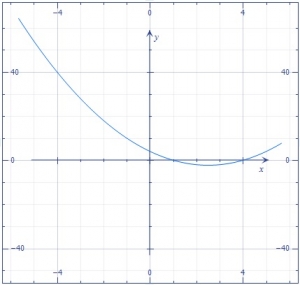 What is the equation of the curve? A. \(y=x^2+6x+4\) B. \(y=x^2-5x-4\) C. \(y=x^2-5x+4\) D. \(y=x^2+5x-4\) Detailed SolutionThe factor for the curve are (x-1)(x-4). The product off the curves gives \(=x^2-5x+4=y\) |
|
| 39. |
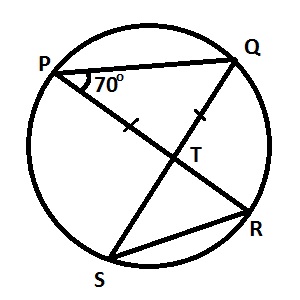 In the diagram PQRS is a circle, |PT| = |QT| and ∠QPT = 70o what is the size of ∠PRS? A. 40o B. 70o C. 80o D. 140o Detailed Solution∠QPT = ∠QTP = 70o. Since ∠QTR = 140o∠PRS = TSR = 1/2(180-40) = 70o |
|
| 40. |
The angle of elevation of the top of a cliff 15 meters high from a landmark is 60o. How far is the landmark from the foot of the cliff? Leave your answer in surd form A. \(15\sqrt{3}m\) B. \(15\sqrt{2}m\) C. \(10\sqrt{3}m\) D. \(5\sqrt{3}m\) Detailed Solution\(tan 60^{\circ} = \frac{15}{x} \Rightarrow x = \frac{15}{tan60^{\circ}\\x = \left(\frac{15}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\right)m \Rightarrow 5\sqrt{3}m\) |
| 31. |
A train moving at a uniform speed covers 36km in 21 minutes. How long does it take to cover 60km? A. 35 mins B. 40 mins C. 45 mins D. 90 mins Detailed SolutionSince 36km in 21 minutes1km in \(\frac{21}{36}\)minutes 60km in \(\left(\frac{21}{36}\times 60\right)\)minutes = \(\frac{70}{2}\)min = 35 mins |
|
| 32. |
The salary of a man was increased in the ratio 40:47. calculate the percentage increase in the salary A. 85.1% B. 58.5% C. 17.5% D. 14.9% Detailed Solution\(\%Increase = \frac{Actual \hspace{1mm}increase}{initial \hspace{1mm}ratio}\times 100\%\)Actual increase = 7; Initial ratio = 40 \(=\left(\frac{7}{40} \times 100\%\right)=\frac{35}{2}=17.5\%\) |
|
| 33. |
A regular polygon has 9 sides. What is the size of one of its exterior angles? A. 20o B. 40o C. 90o D. 140o Detailed SolutionExterior angle \(=\frac{360}{n}\) where n = no of sides\(=\frac{360}{9}=40^{\circ}\) |
|
| 34. |
Simplify: \(\frac{2}{3xy} - \frac{3}{4yz}\) A. \(\frac{2-x}{12xyz}\) B. \(\frac{2z-3x}{12xyz}\) C. \(\frac{4z-3x}{12xyz}\) D. \(\frac{8z-9x}{12xyz}\) Detailed Solution\(\frac{2}{3xy} - \frac{3}{yz} = \frac{2(4)-3(3x)}{12xyz} = \frac{8z-9x}{12xyz}\) |
|
| 35. |
The total surface area of the walls of a room 7m long, 5m wide and xm high is 96m2. Find the value of x A. \(\frac{2}{3}\) B. 2 C. 4 D. 8 Detailed SolutionT.S.A of the wall \(=2(7\times 5 + 7 \times x + 5 \times x) = 96\\70 + 14x + 10x = 96 \Rightarrow 24x = 96-70=26\\ x = \frac{26}{24}=\frac{13}{12}\) |
| 36. |
For what values of y is the expression \(\frac{6y-1}{y^2 - y-6}\) A. \(\frac{1}{6}, \frac{1}{4}\) B. 3, -2 C. -3, 2 D. 0,1 Detailed SolutionThe expression is not defines when y2 - y - 6 = 0=> y2 - 3y + 2y - 6 = 0 => (y-3)(y+2) = 0 => y -3 = 0 or y + 2 = 0 => y = 3 or -2 |
|
| 37. |
 What are the roots of the equation? A. -1 and 1 B. 4 and 1 C. 1 and 4 D. 4 and 4 Detailed SolutionThe two points of contact of the curve with the x-axis are x = 1 and x = 4. The roots of the equation are x = 1 and x = 4 |
|
| 38. |
 What is the equation of the curve? A. \(y=x^2+6x+4\) B. \(y=x^2-5x-4\) C. \(y=x^2-5x+4\) D. \(y=x^2+5x-4\) Detailed SolutionThe factor for the curve are (x-1)(x-4). The product off the curves gives \(=x^2-5x+4=y\) |
|
| 39. |
 In the diagram PQRS is a circle, |PT| = |QT| and ∠QPT = 70o what is the size of ∠PRS? A. 40o B. 70o C. 80o D. 140o Detailed Solution∠QPT = ∠QTP = 70o. Since ∠QTR = 140o∠PRS = TSR = 1/2(180-40) = 70o |
|
| 40. |
The angle of elevation of the top of a cliff 15 meters high from a landmark is 60o. How far is the landmark from the foot of the cliff? Leave your answer in surd form A. \(15\sqrt{3}m\) B. \(15\sqrt{2}m\) C. \(10\sqrt{3}m\) D. \(5\sqrt{3}m\) Detailed Solution\(tan 60^{\circ} = \frac{15}{x} \Rightarrow x = \frac{15}{tan60^{\circ}\\x = \left(\frac{15}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\right)m \Rightarrow 5\sqrt{3}m\) |