
Mathematics (Core)
Paper 1 | Objectives | 45 Questions
JAMB Exam
Year: 2004
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated

Paper 1 | Objectives | 45 Questions
JAMB Exam
Year: 2004
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
12 Most Effective Ways to Pass Any Exams Without Studying Hard even when you don't have enough time.
Make sure you study hard but not into the late-night hours to give your body the enough rest you need.
Managing Stress and anxiety in exams, 10 tips and strategies for Coping exam stress and test anxiety.
| # | Question | Ans |
|---|---|---|
| 1. |
An arc of a circle of length 22 cm subtends an angle of 3x° at the center of the circle. Find the value of x if the diameter of the circle is 14 cm A. 60o B. 120o C. 180o D. 30o
Show Content
Detailed Solution\( ARC\hspace{1mm}length = (\frac{\theta}{360})\times 2\pi r\\22=\frac{3x}{360}\times \left(2 \times(\frac{22}{7})\times(\frac{7}{1})\right)\\3x = 180\\x = \frac{180}{3}\\x = 60^{\circ}\) |
|
| 2. |
Find the value of α2 + β2 if α + β = 2 and the distance between points (1, α) and (β, 1)is 3 units A. 14 B. 3 C. 5 D. 11
Show Content
Detailed Solution\(PQ = \sqrt{(β - 1)^{2} + (1 - α)^{2}}\\3 =\sqrt{(β^{2} -2β^{2} + 1 + 1 - 2α + α^{2})}\\ 3 = \sqrt{(α^{2} + β^{2} - 2α + 2β + 2)}\\ 3 = \sqrt{(α^{2} + β^{2} - 2(α + β) + 2)}\\ 3 = \sqrt{(α^{2} + β^{2} - 2 * 2 + 2)}\\ 3 = \sqrt{(α^{2} + β^{2} - 2)}\\ 9 = (α^{2} + β^{2} - 2)\\ α^{2} + β^{2} = 9 + 2\\ α^{2} + β^{2} = 11\) |
|
| 3. |
The sum of the interior angles of a pentagon is 6x + 6y. Find y in the terms of x A. y = 90 - x B. y = 150 - x C. y = 60 - x D. y = 120 -x
Show Content
Detailed Solution6x + 6y = (n - 2) 1806x + 6y= (5 - 2) 180 6(x + y) = 3 * 180 x + y = (3 * 180)/6 x + y = 90o y = 90 - x |
|
| 4. |
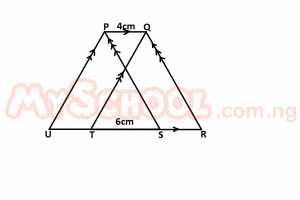 In the diagram above, PQ = 4 cm and TS = 6 cm. If the area of parallelogram PQTU is 32 cm\(^2\), find the area of the trapezium PQRU A. 60 cm2 B. 72 cm2 C. 48 cm2 D. 24 cm2
Show Content
Detailed SolutionArea of parallelogram PQTU = base * height32 = 4 * h w = 32/4 w = 8 ∴ = Area of Trapezium PQRU = (1/2)(4 + 14) *8 = 1/2 * (18 * 8) = 72 cm\(^2\) |
|
| 5. |
Find the midpoint of the line joining P(-3, 5) and Q(5, -3). A. (1, 1) B. (2, 2) C. (4, 4) D. (4, -4)
Show Content
Detailed Solution\(Mid point = \frac{(x_1 + x_2)}{2} ; \frac{(y_1 + y_2)}{2}\\= \frac{(-3 + 5)}{2} ; \frac{(5 - 3)}{2}\\ = \frac{2}{2} ; \frac{2}{2}\\ = (1, 1)\) |
|
| 6. |
Determine the locus of a point inside a square PQRS which is eqidistant from PQ and QR A. The diagonal QS B. the perpendicular bisector of PQ C. The diagonal PR D. side SR
Show Content
Detailed SolutionThe diagonal QS bisects the angle formed by PQ and QR∴ [A] |
|
| 7. |
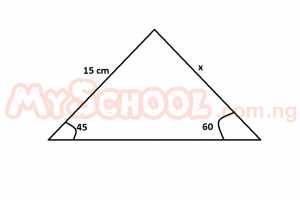 Find the value of x in the figure above A. 15√6 B. 20√6 C. 3√6 D. 5√6
Show Content
Detailed Solution\(\frac{X}{sin45}=\frac{15}{sin60}\\X=\frac{15sin45}{sin60}\\X=\frac{15\times(\frac{1}{\sqrt{2}})}{\sqrt{\frac{3}{2}}}\\X=\frac{15}{\sqrt{2}}\times\frac{2}{\sqrt{3}}\\X=\frac{30}{\sqrt{6}}\\X=\frac{30}{\sqrt{6}}\times\frac{\sqrt{6}}{\sqrt{6}}=\frac{30\sqrt{6}}{6}=5\sqrt{6}\) |
|
| 8. |
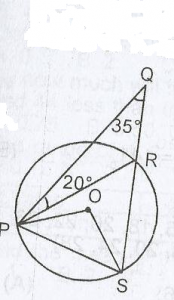 P, R and S lie on a circle center as shown above while Q lies outside the circle. Find ∠PSO A. 45o B. 55o C. 35o D. 40o
Show Content
Detailed Solutionxo = 35 + 29 (Exterior angle = sum of two interior opposite angles)x = 55o (∠ at the center twice ∠ at circumference) y = 110o ∠PSO = ∠SPO (base ∠S of 1sc Δ b/c PO = SO) ∴ ∠PSO = (180 - 110)/2 = 35o |
|
| 9. |
The locus of a point which is 5 cm from the line LM is a A. line distance 10 cm from LM and parallel to LM B. pair of line on opposite sides of LM and parallel to it, each distance 5 cm from LM C. line parallel to LM and 5 cm from LM D. pair of parallel lines on one side of LM and parallel to LM
Show Content
Detailed SolutionThe locus of a point which is 5cm from the line LM is a pair of lines on opposite sides of LM and parallel to it, each distance 5cm from LM. |
Preview displays only 9 out of the 45 Questions