Mathematics (Core)
Paper 1 | Objectives | 62 Questions
JAMB Exam
Year: 2018
Level: SHS
Time:
Type: Question Paper
Answers provided
FREE
No description provided
Feedbacks
This paper is yet to be rated
Paper 1 | Objectives | 62 Questions
JAMB Exam
Year: 2018
Level: SHS
Time:
Type: Question Paper
Answers provided
No description provided
This paper is yet to be rated
| # | Question | Ans |
|---|---|---|
| 1. |
In a class of 40 students, 32 offer Mathematics, 24 offer Physics and 4 offer neither Mathematics nor Physics. How many offer both Mathematics and Physics? A. 4 B. 8 C. 16 D. 20 Detailed SolutionLet the number of people that offer both Mathematics and Physics = yThen, \((32 - y) + y + (24 - y) + 4 = 40\) \(60 - y = 40 \implies y = 20\) \(\therefore\) 20 students offer both Mathematics and Physics. There is an explanation video available below. |
|
| 2. |
Find the values of x for which\(\frac {x+2}{4}\) - \(\frac{2x - 3}{3}\) < 4 A. x < 8 B. x > -6 C. x < 4 D. x > -3 Detailed Solution\(\frac {x+2}{4}\) - \(\frac{2x - 3}{3} < 4\)\(\frac{3(x + 2) - 4(2x - 3)}{12} < 4\) \(3x + 6 - 8x + 12 < 48 \) \(18 - 5x < 48 \implies -5x < 30\) \(\therefore x > -6\) There is an explanation video available below. |
|
| 3. |
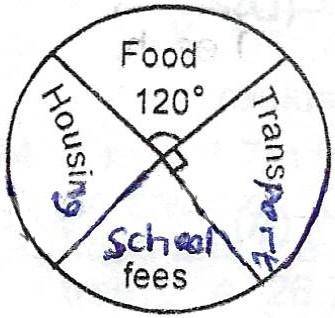 The pie chart shows the monthly expenditure of a public servant. The monthly expenditure on housing is twice that of school fees. How much does the worker spend on housing if his monthly income is N7200? A. 1000 B. 2000 C. 3000 D. 4000 Detailed SolutionLet the angle for school fees = x°Then Housing = 2x° 120° + 90° + x° + 2x° = 360° 3x° = 150° \(\implies\) x° = 50°. Amount spent on housing = \(\frac{100}{360} \times 7200\) = N2000. There is an explanation video available below. |
|
| 4. |
A trader realises 10x - x\(^2\) Naira profit from the sale of x bags of corn. How many bags will give him the maximum profit? A. 7 B. 6 C. 5 D. 4 Detailed SolutionProfit (P) = 10\(_x\) − \(_x\)2Maximum profit can be achieved when the differential of profit with respect to number of bags(x) is 0 i.e. \(\frac{dp}{dx}\) = 0 \(\frac{dp}{dx}\) = 10 - 2x = 0 10 = 2x Then x = \(\frac{10}{2}\) = 5 Answer is C There is an explanation video available below. |
|
| 5. |
If y = 23\(_{five}\) + 101\(_{three}\) , find y, leaving your answer in base two A. 1110 B. 10111 C. 11101 D. 111100 Detailed Solutiony = 23\(_{five}\) + 101\(_{three}\)23\(_{five}\) = \(2 \times 5^1 + 3 \times 5^0\) = 13\(_{ten}\) 101\(_{three}\) = \(1 \times 3^2 + 0 \times 3^1 + 1 \times 3^0\) = 10\(_{ten}\) y\(_{ten}\) = 13\(_{ten}\) + 10\(_{ten}\) = 23\(_{ten}\) = 10111\(_{two}\) There is an explanation video available below. |
|
| 6. |
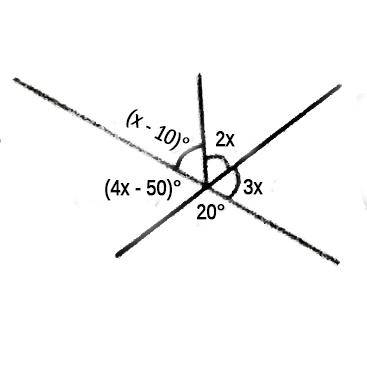 Find the value of x in the diagram A. 10° B. 28° C. 36° D. 40° Detailed SolutionThe diagram shows angles at a point, the total angle at a point is 360x - 10 + 4x - 50 + 2x + 3x + 20 = 360 10x - 40 = 360 10x = 360 + 40 10x = 400 x = \(\frac{400}{10}\) x = 40 There is an explanation video available below. |
|
| 7. |
Solve for t in the equation \(\frac{3}{4}\)t + \(\frac{1}{3}\)(21 - t) = 11 A. \(\frac{9}{13}\) B. \(\frac{7}{13}\) C. 5 D. 9\(\frac{3}{5}\) Detailed Solution\(\frac{3}{4}\) t + \(\frac{1}{3}\) (21 - t) = 11Multiply through by the LCM of 4 and 3 which is 12 12 x(\(\frac{3}{4}\) t) + 12 x (\(\frac{1}{3}\) (21 - t)) = (11 x 12) 9t + 4(21 - t) = 132 9t + 84 - 4t = 132 5t + 84 = 132 5t = 132 - 84 = 48 t = \(\frac{48}{5}\) t = 9 \(\frac{3}{5}\) Answer is D There is an explanation video available below. |
|
| 8. |
A school girl spends \(\frac{1}{4}\) of her pocket money on books and \(\frac{1}{3}\) on dress. What fraction remains? A. \(\frac{5}{6}\) B. \(\frac{7}{12}\) C. \(\frac{5}{12}\) D. \(\frac{1}{6}\) |
|
| 9. |
If \(\frac{x}{a + 1}\) + \(\frac{y}{b}\) = 1. Make y the subject of the relation. A. \(\frac{b(a + 1 - x)}{a + 1}\) B. \(\frac{a + 1}{b(a - x + 1)}\) C. \(\frac{a(b - x + 1)}{b + 1}\) D. \(\frac{b}{a(b - x + 1)}\) |
|
| 10. |
Calculate the total surface area of a cupboard which measures 12cm by 10cm by 8cm A. 1920cm\(^2\) B. 592cm\(^2\) C. 296cm\(^2\) D. 148cm\(^2\) Detailed SolutionTotal surface area of a cupboard is given by the equation A = 2(lb + bh + lh) L = 12, b = 10, h = 8A = 2((12 x 10) + (10 x 8) + (12 x 8)) A = 2(120 + 80 + 96) A = 2 x 296 A = 592cm\(^2\) Answer is B There is an explanation video available below. |
|
| 11. |
Convert 0.04945 to two significant figures A. 0.040 B. 0.049 C. 0.050 D. 0.49 |
|
| 12. |
The probabilities that John and James pass an examination are \(\frac {3}{4}\)and \(\frac {3}{5}\) respectively. Find the probability of both boys failing the examination. A. \(\frac {1}{10}\) B. \(\frac {2}{10}\) C. \(\frac {9}{20}\) D. \(\frac {11}{20}\) Detailed SolutionPr(both John and James passed)= \(\frac {3}{4}\) x \(\frac {3}{5}\) = \(\frac {9}{20}\) Pr(john and james failed)= 1- Pr(john and james passed) = 1 – \(\frac {9}{20}\) = \(\frac {11}{20}\) Answer is D There is an explanation video available below. |
|
| 13. |
An arc of a circle of radius 14cm subtends angle 300° at the centre. Find the perimeter of the sector formed by the arc (take π = \(\frac{22}{7}\)) A. 14.67cm B. 73.33 cm C. 101.33cm D. 513.33cm Detailed SolutionLength of the arc = \(\frac{\theta}{360} \times 2\pi r\)= \(\frac{300}{360} \times 2 \times \frac{22}{7} \times 14\) = \(\frac{220}{3}\) = 73.33 cm Perimeter of the sector = Length of the arc + 2r = 73.33 + 2(14) = 101.33 cm There is an explanation video available below. |
Preview displays only 13 out of the 62 Questions