Year : 
1988
Title : 
Mathematics (Core)
Exam : 
WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

21 - 30 of 41 Questions

# Question Ans
21.

What is the probability of having an odd number in a single toss of a fair die?

A. 1/6

B. 1/3

C. 1/2

D. 2/3

E. 5/6

Detailed Solution

n(S) = 6(odd) = {1, 3, 5}

n(odd) = 3

pr(odd) = \(\frac{n(odd)}{n(S)}\) 3/6 =1/2
22.

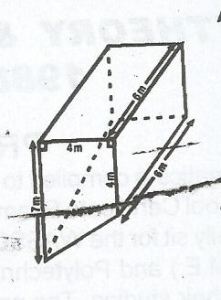A water tank is made with a right-angled trapezium - shaped vertical cross-section so that when it is placed on sloping ground the top of the tank is level. The dimension are given in the diagram above
If the tank is completely filled with water, how many cubic metres can it hold?

A. 66m3

B. 84m3

C. 132m3

D. 168m3

E. 264m3

Detailed Solution

Area of trapezium = 1/2(a+b)h
= 1/2(4 + 7)x4 = 22m2
volume = 22 x 6 = 132m3
23.

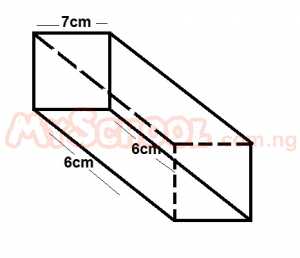A water tank is made with a right-angled trapezium - shaped vertical cross-section so that when it is placed on sloping ground the top of the tank is level. The dimension are given in the diagram above
By what number will you multiply your answer in 22 above to determine the capacity of the tank in liters?

A. 1/10

B. 1

C. 10

D. 100

E. 1000

Detailed Solution

1m = 100cm, 1m3 = (100cm)3 = 106 cm3

but 1000cm4 = 1liter. 106 cm3 = 1000liters.

1m3 = 1000liters.
24.

Evaluate log106 + log1045 - log1027 without using logarithm tables

A. o

B. 1

C. 1.1738

D. 1.3802

E. 10

Detailed Solution

log106 + log1045 - log1027

log10 \(\frac{6 \times 45}{27}\)

= log102 x 5

log1010 = 1
25.

Find the product xy if, x, 3/2, 6/7, y are in G.P

A. 24/49

B. 4/7

C. 9/7

D. 7/4

E. 21/8

Detailed Solution

In GP, when you are given three consecutive terms, say f, g, h, then
\(f \times h = g^2\)
Given: \(x, \frac{3}{2}, \frac{6}{7}, y\), then
\(\frac{6x}{7} = (\frac{3}{2})^2 \implies \frac{6x}{7} = \frac{9}{4} ... (i)\)
Also, \(\frac{3y}{2} = (\frac{6}{7})^2 \implies \frac{3y}{2} = \frac{36}{49} ... (ii)\)
From \(\frac{6x}{7} = \frac{9}{4} \implies x = \frac{9 \times 7}{6 \times 4}\)
\(x = \frac{21}{8}\)
Also, \(\frac{3y}{2} = \frac{36}{49} \implies y = \frac{2 \times 36}{3 \times 49}\)
= \(\frac{24}{49}\)
\(xy = \frac{21}{8} \times \frac{24}{49} = \frac{9}{7}\)
26.

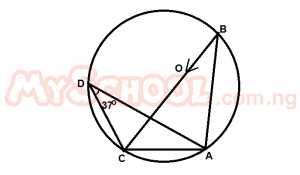In the diagram above, O is the center of the circle, BOC is a diameter and angle ADC is 37o
What is ACB?

A. 147o

B. 127o

C. 65o

D. 53o

E. 37o

Detailed Solution

From the figure \(< ABC = < ADC = 37°\) (angles on the same segment)
\(< BCA = 90°\) (angle in semi-circle)
\(\therefore\) In \(\Delta ABC\), \(< ACB = 180° - (37° + 90°)\)
= 53°
27.

Factorize 5y2 + 2y - 3a2

A. (5y - a) (y + 3a)

B. (5y + a) (y - 3a)

C. 5y2 + a (2y - 3a)

D. (y - a) (5y + 3a)

E. (y + a) (5y - 3a)

Detailed Solution

5y 2 + 5ay - 3ay - 3a 2
5y(y + a) - 3a(y + a)
(y + a) (5y - 3a)
28.

Which of the following is a correct method for constructing an angle of 60o at Q?

A. I only

B. II only

C. III only

D. I and II only

E. II and III only

B
29.

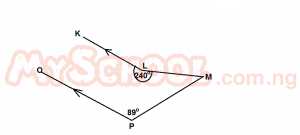IN the diagram above, LK/PQ, reflex angle KLM = 241° and ∠QPM = 89°. What is the value of ∠LMP?

A. 30o

B. 61o

C. 89o

D. 119o

E. 150o

Detailed Solution

Produce ML to R.
From the figure < LRM = 89° (corresponding angles)
In triangle LRM, < LMR = 180° - (61° + 89°)
= 30°
30.

Abidjan is 4o west of Accra and on the same circle of latitude. If the radius of this circle of latitude is 6370km, how far is Abidjan west of Accra, correct to the nearest kilometer? [Take π = 22/7]

A. 222km

B. 445km

C. 890km

D. 5005km

E. 10010km

Detailed Solution

θ/360
* 2πr = Rcos4o


4/360
*
40041/1
21.

What is the probability of having an odd number in a single toss of a fair die?

A. 1/6

B. 1/3

C. 1/2

D. 2/3

E. 5/6

Detailed Solution

n(S) = 6(odd) = {1, 3, 5}

n(odd) = 3

pr(odd) = \(\frac{n(odd)}{n(S)}\) 3/6 =1/2
22.

A water tank is made with a right-angled trapezium - shaped vertical cross-section so that when it is placed on sloping ground the top of the tank is level. The dimension are given in the diagram above
If the tank is completely filled with water, how many cubic metres can it hold?

A. 66m3

B. 84m3

C. 132m3

D. 168m3

E. 264m3

Detailed Solution

Area of trapezium = 1/2(a+b)h
= 1/2(4 + 7)x4 = 22m2
volume = 22 x 6 = 132m3
23.

A water tank is made with a right-angled trapezium - shaped vertical cross-section so that when it is placed on sloping ground the top of the tank is level. The dimension are given in the diagram above
By what number will you multiply your answer in 22 above to determine the capacity of the tank in liters?

A. 1/10

B. 1

C. 10

D. 100

E. 1000

Detailed Solution

1m = 100cm, 1m3 = (100cm)3 = 106 cm3

but 1000cm4 = 1liter. 106 cm3 = 1000liters.

1m3 = 1000liters.
24.

Evaluate log106 + log1045 - log1027 without using logarithm tables

A. o

B. 1

C. 1.1738

D. 1.3802

E. 10

Detailed Solution

log106 + log1045 - log1027

log10 \(\frac{6 \times 45}{27}\)

= log102 x 5

log1010 = 1
25.

Find the product xy if, x, 3/2, 6/7, y are in G.P

A. 24/49

B. 4/7

C. 9/7

D. 7/4

E. 21/8

Detailed Solution

In GP, when you are given three consecutive terms, say f, g, h, then
\(f \times h = g^2\)
Given: \(x, \frac{3}{2}, \frac{6}{7}, y\), then
\(\frac{6x}{7} = (\frac{3}{2})^2 \implies \frac{6x}{7} = \frac{9}{4} ... (i)\)
Also, \(\frac{3y}{2} = (\frac{6}{7})^2 \implies \frac{3y}{2} = \frac{36}{49} ... (ii)\)
From \(\frac{6x}{7} = \frac{9}{4} \implies x = \frac{9 \times 7}{6 \times 4}\)
\(x = \frac{21}{8}\)
Also, \(\frac{3y}{2} = \frac{36}{49} \implies y = \frac{2 \times 36}{3 \times 49}\)
= \(\frac{24}{49}\)
\(xy = \frac{21}{8} \times \frac{24}{49} = \frac{9}{7}\)
26.

In the diagram above, O is the center of the circle, BOC is a diameter and angle ADC is 37o
What is ACB?

A. 147o

B. 127o

C. 65o

D. 53o

E. 37o

Detailed Solution

From the figure \(< ABC = < ADC = 37°\) (angles on the same segment)
\(< BCA = 90°\) (angle in semi-circle)
\(\therefore\) In \(\Delta ABC\), \(< ACB = 180° - (37° + 90°)\)
= 53°
27.

Factorize 5y2 + 2y - 3a2

A. (5y - a) (y + 3a)

B. (5y + a) (y - 3a)

C. 5y2 + a (2y - 3a)

D. (y - a) (5y + 3a)

E. (y + a) (5y - 3a)

Detailed Solution

5y 2 + 5ay - 3ay - 3a 2
5y(y + a) - 3a(y + a)
(y + a) (5y - 3a)
28.

Which of the following is a correct method for constructing an angle of 60o at Q?

A. I only

B. II only

C. III only

D. I and II only

E. II and III only

B
29.

IN the diagram above, LK/PQ, reflex angle KLM = 241° and ∠QPM = 89°. What is the value of ∠LMP?

A. 30o

B. 61o

C. 89o

D. 119o

E. 150o

Detailed Solution

Produce ML to R.
From the figure < LRM = 89° (corresponding angles)
In triangle LRM, < LMR = 180° - (61° + 89°)
= 30°
30.

Abidjan is 4o west of Accra and on the same circle of latitude. If the radius of this circle of latitude is 6370km, how far is Abidjan west of Accra, correct to the nearest kilometer? [Take π = 22/7]

A. 222km

B. 445km

C. 890km

D. 5005km

E. 10010km

Detailed Solution

θ/360
* 2πr = Rcos4o


4/360
*
40041/1