Year :
1993
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
11 - 20 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 11. |
Write as a single fraction: \(\frac{5}{6r} - \frac{3}{4r}\) A. r12 B. 12r C. 16r D. r6 E. 112r Detailed Solution\(\frac{5}{6r} - \frac{3}{4r}\)= \(\frac{10 - 9}{12r}\) = \(\frac{1}{12r}\) |
|
| 12. |
Factorize 2x\(^2\) - 21x + 45 A. (2x - 9)(x - 5) B. (2x-15)(x + 3) C. (2x +15)(x - 3) D. (2x -15(x - 3) E. (2x - 9)(x + 5) Detailed Solution2x\(^2\) - 21x + 45= 2x\(^2\) - 15x - 6x + 45 = x(2x - 15) - 3(2x - 15) = (x - 3)(2x - 15) |
|
| 13. |
Solve the simultaneous equations y = 3x; 4y - 5x =14 A. .-2,-6 B. 2,6 C. 2,-6 D. -2,6 E. -1,-3 Detailed Solutiony = 3x ... (i);4y - 5x =14 ... (ii) Put 3x for y in (ii). 4(3x) - 5x = 14 12x - 5x = 14 7x = 14 \(\implies\) x = 2. y = 3x = 3(2) = 6 (x, y) = (2, 6) |
|
| 14. |
A sector of a circle of radius 9cm subtends angle 120° at the centre of the circle. Find the area of the sector to the nearest cm\(^2\) [Take π = 22/7] A. 75cm2 B. 84cm2 C. 85cm2 D. 86cm2 E. 95cm2 Detailed Solution
= 120/360 x 22/7 x 81/1 = 84.86 cm\(^2\) \(\approxeq\) 85cm\(^2\) (to the nearest cm) |
|
| 15. |
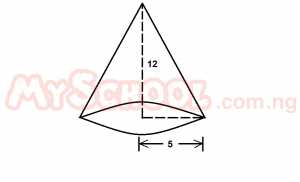
Calculate the total surface area of a cone of height 12cm and base radius 5cm. [Take π = 22/7] A. 180 5/7cm2 B. 240 2/7cm2 C. 235 5/7cm2 D. 282 6/7cm2 E. 361 3/7cm2 Detailed Solution
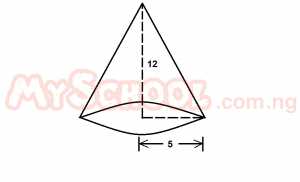 22/7 x 5(13 + 5) 282 6/7cm2 |
|
| 16. |
A cone is 14cm deep and the base radius is 41/2cm. Calculate the volume of water that is exactly half the volume of the cone.[Take π = 22/7] A. 49.5cm3 B. 99cm3 C. 148.5cm3 D. 297cm3 E. 445.5cm3 Detailed SolutionVolume of a cone = \(\frac{1}{3} \pi r^2 h\)r = 4\(\frac{1}{2}\) cm; h = 14 cm Volume of cone = \(\frac{1}{3} \times \frac{22}{7} \times \frac{9}{2} \times \frac{9}{2} \times 14\) = 297 cm\(^3\) When half- filled, the volume of the water = \(\frac{297}{2} = 148.5 cm^3\) |
|
| 17. |
The area and a diagonal of a rhombus are 60 cm\(^2\) and 12 cm respectively. Calculate the length of the other diagonal. A. 5cm B. 6cm C. 10cm D. 12cm E. 15cm Detailed SolutionArea of rhombus = \(\frac{pq}{2}\)where p and q are the two diagonals of the rhombus. \(\therefore 60 = \frac{12 \times q}{2}\) 6q = 60 \(\implies\) q = 10 cm |
|
| 18. |
The angle of a sector of a circle radius 10.5cm is 120°. Find the perimeter of the sector [Take π = 22/7] A. 22cm B. 33.5cm C. 43cm D. 66cm E. 115.5cm Detailed SolutionPerimeter of a sector = \(2r + \frac{\theta}{360} \times 2\pi r\)= \(2(10.5) + \frac{120}{360} \times 2 \times \frac{22}{7} \times 10.5\) = \(21 + 22\) = 43 cm |
|
| 19. |
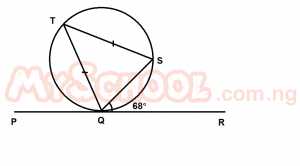 In the diagram, PQR is a tangent to the circle QST at Q. If |QT| = |ST| and ∠SQR = 68°, find ∠PQT. A. 34o B. 48o C. 56o D. 68o E. 73o Detailed Solution< STQ = < SQR = 68° (alternate segment)\(\therefore\) < STQ = 68° < TQS = \(\frac{180° - 68°}{2}\) = \(\frac{112}{2} = 56°\) \(\therefore\) < PQT = 180° - (68° + 56°) = 180° - 124° = 56° |
|
| 20. |
The sum of an interior angles of a regular polygon is 30 right angles. How many sides has the polygon? A. 34 sides B. 30 sides C. 26 sides D. 17 sides E. 15 sides Detailed SolutionSum of interior angles in a polygon = \((2n - 4) \times 90°\)\(\therefore (2n - 4) \times 90° = 30 \times 90°\) \(\implies 2n - 4 = 30 \) \(2n = 34 \implies n = 17\) The polygon has 17 sides. |
| 11. |
Write as a single fraction: \(\frac{5}{6r} - \frac{3}{4r}\) A. r12 B. 12r C. 16r D. r6 E. 112r Detailed Solution\(\frac{5}{6r} - \frac{3}{4r}\)= \(\frac{10 - 9}{12r}\) = \(\frac{1}{12r}\) |
|
| 12. |
Factorize 2x\(^2\) - 21x + 45 A. (2x - 9)(x - 5) B. (2x-15)(x + 3) C. (2x +15)(x - 3) D. (2x -15(x - 3) E. (2x - 9)(x + 5) Detailed Solution2x\(^2\) - 21x + 45= 2x\(^2\) - 15x - 6x + 45 = x(2x - 15) - 3(2x - 15) = (x - 3)(2x - 15) |
|
| 13. |
Solve the simultaneous equations y = 3x; 4y - 5x =14 A. .-2,-6 B. 2,6 C. 2,-6 D. -2,6 E. -1,-3 Detailed Solutiony = 3x ... (i);4y - 5x =14 ... (ii) Put 3x for y in (ii). 4(3x) - 5x = 14 12x - 5x = 14 7x = 14 \(\implies\) x = 2. y = 3x = 3(2) = 6 (x, y) = (2, 6) |
|
| 14. |
A sector of a circle of radius 9cm subtends angle 120° at the centre of the circle. Find the area of the sector to the nearest cm\(^2\) [Take π = 22/7] A. 75cm2 B. 84cm2 C. 85cm2 D. 86cm2 E. 95cm2 Detailed Solution
= 120/360 x 22/7 x 81/1 = 84.86 cm\(^2\) \(\approxeq\) 85cm\(^2\) (to the nearest cm) |
|
| 15. |
Calculate the total surface area of a cone of height 12cm and base radius 5cm. [Take π = 22/7] A. 180 5/7cm2 B. 240 2/7cm2 C. 235 5/7cm2 D. 282 6/7cm2 E. 361 3/7cm2 Detailed Solution
 22/7 x 5(13 + 5) 282 6/7cm2 |
| 16. |
A cone is 14cm deep and the base radius is 41/2cm. Calculate the volume of water that is exactly half the volume of the cone.[Take π = 22/7] A. 49.5cm3 B. 99cm3 C. 148.5cm3 D. 297cm3 E. 445.5cm3 Detailed SolutionVolume of a cone = \(\frac{1}{3} \pi r^2 h\)r = 4\(\frac{1}{2}\) cm; h = 14 cm Volume of cone = \(\frac{1}{3} \times \frac{22}{7} \times \frac{9}{2} \times \frac{9}{2} \times 14\) = 297 cm\(^3\) When half- filled, the volume of the water = \(\frac{297}{2} = 148.5 cm^3\) |
|
| 17. |
The area and a diagonal of a rhombus are 60 cm\(^2\) and 12 cm respectively. Calculate the length of the other diagonal. A. 5cm B. 6cm C. 10cm D. 12cm E. 15cm Detailed SolutionArea of rhombus = \(\frac{pq}{2}\)where p and q are the two diagonals of the rhombus. \(\therefore 60 = \frac{12 \times q}{2}\) 6q = 60 \(\implies\) q = 10 cm |
|
| 18. |
The angle of a sector of a circle radius 10.5cm is 120°. Find the perimeter of the sector [Take π = 22/7] A. 22cm B. 33.5cm C. 43cm D. 66cm E. 115.5cm Detailed SolutionPerimeter of a sector = \(2r + \frac{\theta}{360} \times 2\pi r\)= \(2(10.5) + \frac{120}{360} \times 2 \times \frac{22}{7} \times 10.5\) = \(21 + 22\) = 43 cm |
|
| 19. |
 In the diagram, PQR is a tangent to the circle QST at Q. If |QT| = |ST| and ∠SQR = 68°, find ∠PQT. A. 34o B. 48o C. 56o D. 68o E. 73o Detailed Solution< STQ = < SQR = 68° (alternate segment)\(\therefore\) < STQ = 68° < TQS = \(\frac{180° - 68°}{2}\) = \(\frac{112}{2} = 56°\) \(\therefore\) < PQT = 180° - (68° + 56°) = 180° - 124° = 56° |
|
| 20. |
The sum of an interior angles of a regular polygon is 30 right angles. How many sides has the polygon? A. 34 sides B. 30 sides C. 26 sides D. 17 sides E. 15 sides Detailed SolutionSum of interior angles in a polygon = \((2n - 4) \times 90°\)\(\therefore (2n - 4) \times 90° = 30 \times 90°\) \(\implies 2n - 4 = 30 \) \(2n = 34 \implies n = 17\) The polygon has 17 sides. |