Year :
2009
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 46 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
Find the quadratic equation whose roots are -\(\frac{1}{2}\) and 3 A. 2x2 - 2x + 3 = 0 B. 2x2 - 2x - 3 = 0 C. 2x2 - 5x - 3 = 0 D. 3x2 - 5x - 3 = 0 Detailed Solutionx = \(\frac{-1}{2}\)x = 3 2x = -1, x = 3; 2x + 1 = 0 x - 3 = 0 (2x + 1)(x - 3) = 0 2x2 - 6x + x - 3 = 0 2x2 - 5x - 3 = 0 |
|
| 32. |
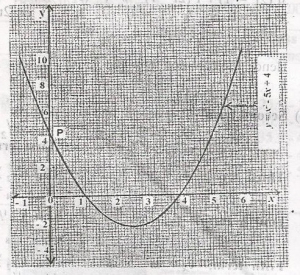 The following is the graph of a quadratic friction, find the co-ordinates of point P A. (0, 4) B. (4, 0) C. (0, -4) D. (-4, 0) |
A |
| 33. |
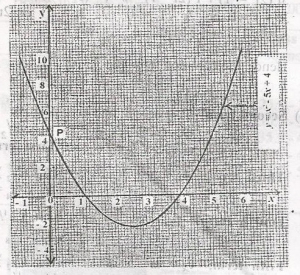 The following is the graph of a quadratic friction, find the value of x when y = 0 A. 1, 2 B. 1, 4 C. 2, 3 D. 1, 6 Detailed Solutionwhen y = 0, value of x = roots of the equationx2 - 5x + 4 = 0 x = 1, 4 (see graph) |
|
| 34. |
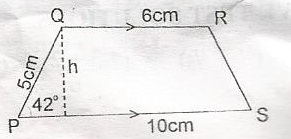
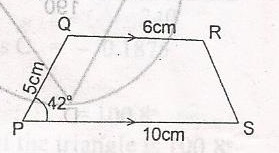 PQRS is a trapezuim. QR//PS, /PQ/ = 5cm, /OR/ = 6cm, /PS/ = 10cm and angle QPS = 42o. Calculate the perpendicular distance between the parallel sides A. 3.35cm B. 3.73cm C. 4.50cm D. 4.62cm Detailed Solution
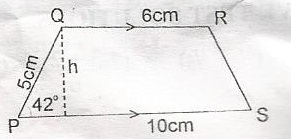 \(\frac{h}{5cm}\) = sin 45o h = 5cm x 0.6691 = 3.35cm |
|
| 35. |
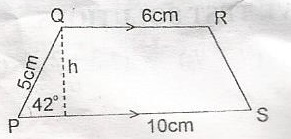
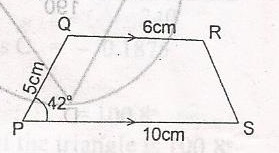 PQRS is a trapezium. QR//PS, /PQ/ = 5cm, /OR/ = 6cm, /PS/ = 10cm and angle QPS = 42o. Calculate, correct to the nearest cm2, the area of the trapezium (h = 3.35cm2 ) A. 27cm2 B. 30cm2 C. 36cm2 D. 37cm2 Detailed Solution
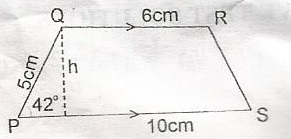 where a = QR = 6cm b = PA = 10cm Area = \(\frac{1}{2}(6 + 10)\) x 3.35cm2 = \(\frac{1}{2}(16)\) x 3.35cm2 = 26.8cm2 = 27cm2 (approx.) |
|
| 36. |
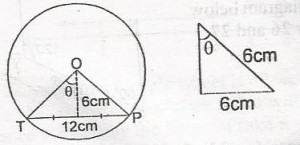
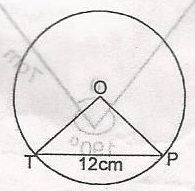 In the diagram, /TP/ = 12cm and it is 6cm from O, the centre of the circle, Calculate < TOP A. 120o B. 90o C. 60o D. 45o Detailed Solution
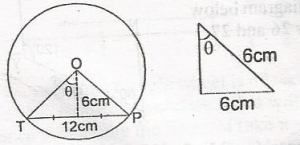 \(\theta\) = tab - 1(1) = 45o < top = 20 = 2 x 45o = 90o |
|
| 37. |
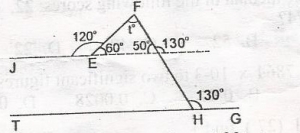
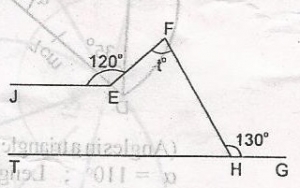 In the diagram, IG is parallel to JE, JEF = 120o and FHG = 130o, fins the angle marked t A. 40o B. 70o C. 80o D. 100o Detailed Solution
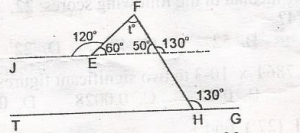 t = 180o - 110o t = 70o |
|
| 38. |
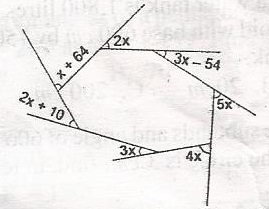
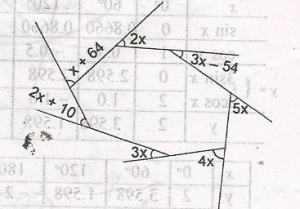 Find the value of x in the diagram A. 50o B. 30o C. 22o D. 17o Detailed Solution
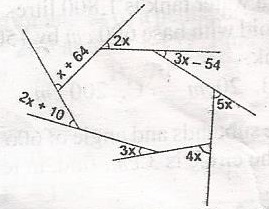 (x + 64) + 2x + (3x - 54) + 5x + 4x + 3x + (2x + 10) = 360o 20x + 20 = 360o 20x + 360 - 20 = 340o x = \(\frac{340}{20}\) x = 17o |
|
| 39. |
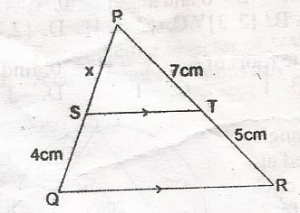
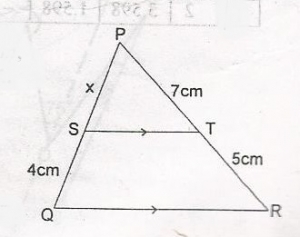 In the diagram, \SQ\ = 4cm, \PT\ = 7cm. /TR/ = 5cm and ST//OR. If /SP/ = xcm, find the value of x A. 5.6 B. 6.5 C. 6.6 D. 6.8 Detailed Solution
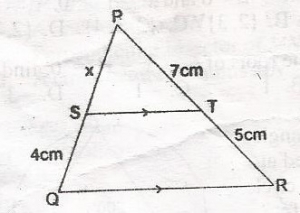 \(\frac{x}{4 + x} = \frac{7}{7 + 5}\) \(\frac{x}{4 + x} = \frac{7}{12}\) (2x = 7)(4 + x); 12x = 28 + 7x 12x - 7x = 28 5x = 28 x = \(\frac{28}{5}\) x = 5.6 |
|
| 40. |
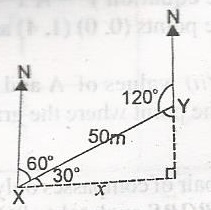
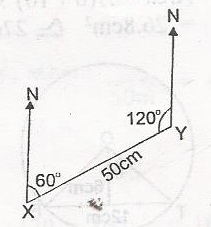 Using the diagram, find the bearing of X from Y A. 300o B. 240o C. 120o D. 60o Detailed Solution
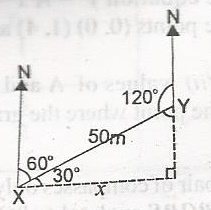 = 360 - 120 = 240 |
| 31. |
Find the quadratic equation whose roots are -\(\frac{1}{2}\) and 3 A. 2x2 - 2x + 3 = 0 B. 2x2 - 2x - 3 = 0 C. 2x2 - 5x - 3 = 0 D. 3x2 - 5x - 3 = 0 Detailed Solutionx = \(\frac{-1}{2}\)x = 3 2x = -1, x = 3; 2x + 1 = 0 x - 3 = 0 (2x + 1)(x - 3) = 0 2x2 - 6x + x - 3 = 0 2x2 - 5x - 3 = 0 |
|
| 32. |
 The following is the graph of a quadratic friction, find the co-ordinates of point P A. (0, 4) B. (4, 0) C. (0, -4) D. (-4, 0) |
A |
| 33. |
 The following is the graph of a quadratic friction, find the value of x when y = 0 A. 1, 2 B. 1, 4 C. 2, 3 D. 1, 6 Detailed Solutionwhen y = 0, value of x = roots of the equationx2 - 5x + 4 = 0 x = 1, 4 (see graph) |
|
| 34. |
 PQRS is a trapezuim. QR//PS, /PQ/ = 5cm, /OR/ = 6cm, /PS/ = 10cm and angle QPS = 42o. Calculate the perpendicular distance between the parallel sides A. 3.35cm B. 3.73cm C. 4.50cm D. 4.62cm Detailed Solution
 \(\frac{h}{5cm}\) = sin 45o h = 5cm x 0.6691 = 3.35cm |
|
| 35. |
 PQRS is a trapezium. QR//PS, /PQ/ = 5cm, /OR/ = 6cm, /PS/ = 10cm and angle QPS = 42o. Calculate, correct to the nearest cm2, the area of the trapezium (h = 3.35cm2 ) A. 27cm2 B. 30cm2 C. 36cm2 D. 37cm2 Detailed Solution
 where a = QR = 6cm b = PA = 10cm Area = \(\frac{1}{2}(6 + 10)\) x 3.35cm2 = \(\frac{1}{2}(16)\) x 3.35cm2 = 26.8cm2 = 27cm2 (approx.) |
| 36. |
 In the diagram, /TP/ = 12cm and it is 6cm from O, the centre of the circle, Calculate < TOP A. 120o B. 90o C. 60o D. 45o Detailed Solution
 \(\theta\) = tab - 1(1) = 45o < top = 20 = 2 x 45o = 90o |
|
| 37. |
 In the diagram, IG is parallel to JE, JEF = 120o and FHG = 130o, fins the angle marked t A. 40o B. 70o C. 80o D. 100o Detailed Solution
 t = 180o - 110o t = 70o |
|
| 38. |
 Find the value of x in the diagram A. 50o B. 30o C. 22o D. 17o Detailed Solution
 (x + 64) + 2x + (3x - 54) + 5x + 4x + 3x + (2x + 10) = 360o 20x + 20 = 360o 20x + 360 - 20 = 340o x = \(\frac{340}{20}\) x = 17o |
|
| 39. |
 In the diagram, \SQ\ = 4cm, \PT\ = 7cm. /TR/ = 5cm and ST//OR. If /SP/ = xcm, find the value of x A. 5.6 B. 6.5 C. 6.6 D. 6.8 Detailed Solution
 \(\frac{x}{4 + x} = \frac{7}{7 + 5}\) \(\frac{x}{4 + x} = \frac{7}{12}\) (2x = 7)(4 + x); 12x = 28 + 7x 12x - 7x = 28 5x = 28 x = \(\frac{28}{5}\) x = 5.6 |
|
| 40. |
 Using the diagram, find the bearing of X from Y A. 300o B. 240o C. 120o D. 60o Detailed Solution
 = 360 - 120 = 240 |