Year :
2020
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 40 Questions
| # | Question | Ans |
|---|---|---|
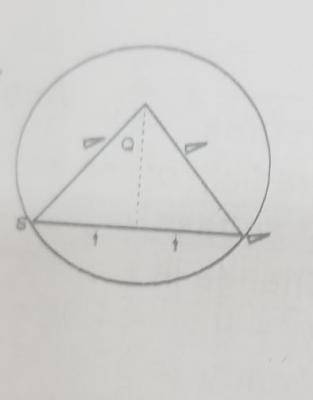
| 31. |
The chord ST of a circle is equal to the radius r of the circle. Find the length of arc ST A. \(\frac{\pi r}{3}\) B. \(\frac{\pi r}{2}\) C. \(\frac{\pi r}{12}\) D. \(\frac{\pi r}{6}\) Detailed Solution
\(\theta\) = sin\(^{-1}\) (\(\frac{1}{2}\)) = 30\(^o\) = 60\(^o\) Length of arc (minor) ST = \(\frac{\theta}{360}\) x 2\(\pi r\) \(\frac{60}{360} \times 2 \pi \times r = \frac{\pi}{3}\) There is an explanation video available below. |
|
| 32. |
A sector of circle of radius 7.2cm which substends an angle of 300\(^o\) at the centre is used to form a cone. What s the radius of the base of the cone? A. 8cm B. 9cm C. 6cm D. 7cm |
|
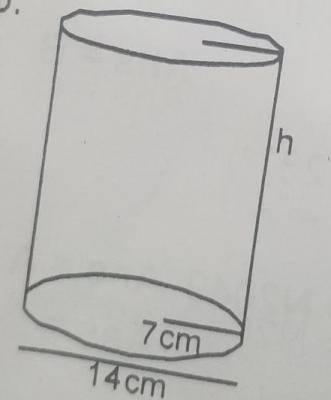
| 33. |
A cylindrical tank has a capacity of 3080m\(^3\). What is the depth of the tank if the diameter of its base is 14m? A. 25m B. 23m C. 22m D. 20m Detailed Solution
r = 7cm V = V\(\pi r^2h\) h = \(\frac{V}{\pi r^2} = \frac{3080}{\frac{22}{7} \times 49}\) \(\frac{3080}{54}\) = 20cm There is an explanation video available below. |
|
| 34. |
The acres for rice, pineapple, cassava, cocoa and palm oil in a certain district are given respectively as 2, 5, 3, 11 and 9. What is the angle of the sector of cassava in a pie chart? A. 180\(^o\) B. 36\(^o\) C. 60\(^o\) D. 108\(^o\) Detailed SolutionTotal number of acres = 2 + 5 + 3 + 11 + 9 = 30The angle of acres = 2 + 5 + 3 + 11 + 9 = 30 The angle of the sector for cassava in a pie chart = \(\frac{3}{30} \times 360^o = 36^o\) There is an explanation video available below. |
|
| 35. |
Three consecutive terms of a geometric progression are give as n - 2, n and n + 3. Find the common ratio A. \(\frac{3}{2}\) B. \(\frac{2}{3}\) C. \(\frac{1}{2}\) D. \(\frac{1}{4}\) Detailed Solution\(\frac{h}{n - 2} = \frac{n + 3}{n}\)n\(^2\) = (n + 3) (n - 2) n\(^2\) = n\(^2\) + n - 6 n\(^2\) + n - 6 - n\(^2\) = 0 n - 6 = 0 n = 6 Common ratio: \(\frac{n}{n - 2} = \frac{6}{6 - 2} = \frac{6}{4}\) = \(\frac{3}{2}\) There is an explanation video available below. |
|
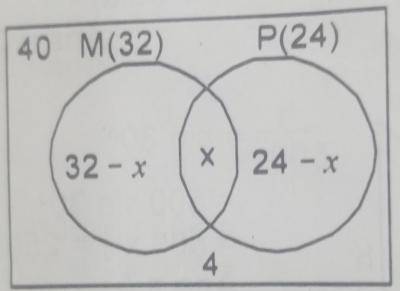
| 36. |
In a class of 40 students, 32 offer mathematics, 24 offer physics and 4 offer neither mathematics nor physics. How many offer both mathematics and physics? A. 4 B. 8 C. 16 D. 20 Detailed Solution
40 = 60 - x x = 60 - 40 x = 20 There is an explanation video available below. |
|
| 37. |
The sum of the interior angle of pentagon is 6x + 6y. Find y in terms of x. A. y = 6 - x B. y = 90 - x C. y = 120 - x D. y = 150 - x Detailed SolutionSum of interior angles = (2n - 4) 90\(^o\)For perntagon, n = 5 Sum of interior angles = 6 x 90\(^o\) = 540\(^o\) 6x + 6y = 540\(^o\) 6(x + y) = 540\(^o\) x + y = \(\frac{540^o}{6}\) = 90\(^o\) y = 90\(^o\) y = 90 - x There is an explanation video available below. |
|
| 38. |
The mean age group of some students is 15years. When the age of a teacher, 45 years old, is added to the ages of the students, the mean of their ages become 18 years. Find the number of students in the group. A. 7 B. 9 C. 15 D. 42 Detailed Solutionx \(\frac{\sum x}{N}\)15 = \(\frac{\sum x }{N}\) \(\sum x\) = 15N........(i) y = \(\frac{\sum y}{Ny} = \frac{\sum x + 45}{N + 1}\) \(\frac{18}{1} = \frac{15N + 45}{N + 1}\) 18(N + 1) = 15N + 45 18N + 18 = 15N + 45 18N - 15N = 45 - 18 3N = 27 N = \(\frac{27}{3}\) = 9 There is an explanation video available below. |
|
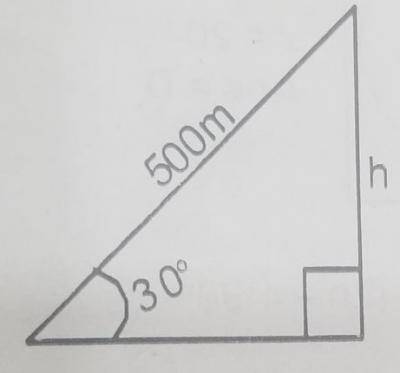
| 39. |
A surveyor walks 500m up a hill which slopes at an angle of 30\(^o\). Calculate the vertical height through which he rises A. 252m B. 500m C. 250m D. 255m Detailed Solution
= 500 sin 30\(^o\) = 500 x \(\frac{1}{2}\) = 250m There is an explanation video available below. |
|
| 40. |
Find the non-zero positive value of x which satisfies the equation \(\begin{bmatrix} x & 1 & 0 \\ 1 & x & 1 \\ 0 & 1 & x \end{bmatrix}\) = 0 A. 2 B. \(\sqrt{3}\) C. \(\sqrt{2}\) D. 1 |
| 31. |
The chord ST of a circle is equal to the radius r of the circle. Find the length of arc ST A. \(\frac{\pi r}{3}\) B. \(\frac{\pi r}{2}\) C. \(\frac{\pi r}{12}\) D. \(\frac{\pi r}{6}\) Detailed Solution
\(\theta\) = sin\(^{-1}\) (\(\frac{1}{2}\)) = 30\(^o\) = 60\(^o\) Length of arc (minor) ST = \(\frac{\theta}{360}\) x 2\(\pi r\) \(\frac{60}{360} \times 2 \pi \times r = \frac{\pi}{3}\) There is an explanation video available below. |
|
| 32. |
A sector of circle of radius 7.2cm which substends an angle of 300\(^o\) at the centre is used to form a cone. What s the radius of the base of the cone? A. 8cm B. 9cm C. 6cm D. 7cm |
|
| 33. |
A cylindrical tank has a capacity of 3080m\(^3\). What is the depth of the tank if the diameter of its base is 14m? A. 25m B. 23m C. 22m D. 20m Detailed Solution
r = 7cm V = V\(\pi r^2h\) h = \(\frac{V}{\pi r^2} = \frac{3080}{\frac{22}{7} \times 49}\) \(\frac{3080}{54}\) = 20cm There is an explanation video available below. |
|
| 34. |
The acres for rice, pineapple, cassava, cocoa and palm oil in a certain district are given respectively as 2, 5, 3, 11 and 9. What is the angle of the sector of cassava in a pie chart? A. 180\(^o\) B. 36\(^o\) C. 60\(^o\) D. 108\(^o\) Detailed SolutionTotal number of acres = 2 + 5 + 3 + 11 + 9 = 30The angle of acres = 2 + 5 + 3 + 11 + 9 = 30 The angle of the sector for cassava in a pie chart = \(\frac{3}{30} \times 360^o = 36^o\) There is an explanation video available below. |
|
| 35. |
Three consecutive terms of a geometric progression are give as n - 2, n and n + 3. Find the common ratio A. \(\frac{3}{2}\) B. \(\frac{2}{3}\) C. \(\frac{1}{2}\) D. \(\frac{1}{4}\) Detailed Solution\(\frac{h}{n - 2} = \frac{n + 3}{n}\)n\(^2\) = (n + 3) (n - 2) n\(^2\) = n\(^2\) + n - 6 n\(^2\) + n - 6 - n\(^2\) = 0 n - 6 = 0 n = 6 Common ratio: \(\frac{n}{n - 2} = \frac{6}{6 - 2} = \frac{6}{4}\) = \(\frac{3}{2}\) There is an explanation video available below. |
| 36. |
In a class of 40 students, 32 offer mathematics, 24 offer physics and 4 offer neither mathematics nor physics. How many offer both mathematics and physics? A. 4 B. 8 C. 16 D. 20 Detailed Solution
40 = 60 - x x = 60 - 40 x = 20 There is an explanation video available below. |
|
| 37. |
The sum of the interior angle of pentagon is 6x + 6y. Find y in terms of x. A. y = 6 - x B. y = 90 - x C. y = 120 - x D. y = 150 - x Detailed SolutionSum of interior angles = (2n - 4) 90\(^o\)For perntagon, n = 5 Sum of interior angles = 6 x 90\(^o\) = 540\(^o\) 6x + 6y = 540\(^o\) 6(x + y) = 540\(^o\) x + y = \(\frac{540^o}{6}\) = 90\(^o\) y = 90\(^o\) y = 90 - x There is an explanation video available below. |
|
| 38. |
The mean age group of some students is 15years. When the age of a teacher, 45 years old, is added to the ages of the students, the mean of their ages become 18 years. Find the number of students in the group. A. 7 B. 9 C. 15 D. 42 Detailed Solutionx \(\frac{\sum x}{N}\)15 = \(\frac{\sum x }{N}\) \(\sum x\) = 15N........(i) y = \(\frac{\sum y}{Ny} = \frac{\sum x + 45}{N + 1}\) \(\frac{18}{1} = \frac{15N + 45}{N + 1}\) 18(N + 1) = 15N + 45 18N + 18 = 15N + 45 18N - 15N = 45 - 18 3N = 27 N = \(\frac{27}{3}\) = 9 There is an explanation video available below. |
|
| 39. |
A surveyor walks 500m up a hill which slopes at an angle of 30\(^o\). Calculate the vertical height through which he rises A. 252m B. 500m C. 250m D. 255m Detailed Solution
= 500 sin 30\(^o\) = 500 x \(\frac{1}{2}\) = 250m There is an explanation video available below. |
|
| 40. |
Find the non-zero positive value of x which satisfies the equation \(\begin{bmatrix} x & 1 & 0 \\ 1 & x & 1 \\ 0 & 1 & x \end{bmatrix}\) = 0 A. 2 B. \(\sqrt{3}\) C. \(\sqrt{2}\) D. 1 |