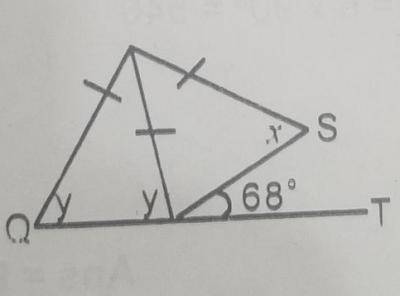Year :
2020
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
11 - 20 of 40 Questions
| # | Question | Ans |
|---|---|---|
| 11. |
If log\(_{10}\)2 = 0.3010 and log\(_{10}\)3 = 0.4771, eventually without using the logarithm tables, log\(_{10}\)4.5 A. 0.3010 B. 0.4771 C. 0.6532 D. 0.9542 Detailed Solutionlog\(_{10}\)2 = 0.3010 and log\(_{10}\)3 = 04771log\(_{10} 4.5 = log_{10}\) (\(\frac{3 \times 3}{2}\)) log\(_{10}\) 3 + log\(_{10}\) 3 - log\(_{10}\)2 = 0.4471 + 0.771 - 0.3010 = 0.6532 There is an explanation video available below. |
|
| 12. |
Simplify \(\frac{324 - 4x^2}{2x + 18}\) A. 2(x - 9) B. 2(9 + x) C. 81 - x\(^2\) D. -2(x - 9) Detailed Solution234 - 4x\(^2\) = 18\(^2\) - (2x)\(^2\) = (18 - 2x)(18 + 2x)2x + 18 = 2x + 18 = (2x + 18) 18 - 2x = 2(a - x) or -2(x - a) There is an explanation video available below. |
|
| 13. |
In preparing rice cutlets, a cook used 75g of rice, 40g of margarine, 105g of meat and 20g of bread crumbs. Find the angle of the sector which represent meat in a pie chart? A. 30\(^o\) B. 60\(^o\) C. 112.5\(^o\) D. 157.5\(^o\) Detailed SolutionRice = 75g, Margarine = 40g, Meat = 105gBread = 20g Total = 240 Angle of sector represented by meat = \(\frac{105}{240} \times \frac{360^o}{1}\) = 157.5 There is an explanation video available below. |
|
| 14. |
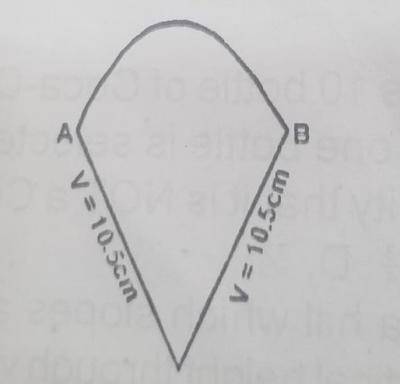
The angle of a sector of a circle radius 10.5 cm is 48\(^o\). Calculate the perimeter of the sector. A. 25.4cm B. 25.4cm C. 25.6cm D. 29.8cm Detailed Solution
= \(\frac{48}{360}\) x 2\(\frac{22}{7}\) x 10.5 = \(\frac{48}{360}\) x 2\(\frac{22}{7}\) x \(\frac{21}{2}\) = \(\frac{4 \times 22 \times 3}{30} \times \frac{88}{10}\) = 8.8cm Perimeter = 8.8 + 2r = 8.8 + 2r = 8.8 + 2(10.5) = 8.8 + 21 = 29.8cm There is an explanation video available below. |
|
| 15. |
What is the product of \(\frac{27}{5}\), \((3)^{-3}\) and (\(\frac{1}{5})^{-1}\)? A. 5 B. 3 C. 1 D. \(\frac{1}{25}\) Detailed Solution\(\frac{27}{5} \times 3^{-3} \times \frac{(1)^{-1}}{5}\)= \(\frac{27}{5} \times \frac{1}{3^3} \times \frac{1}{\frac{1}{5}}\) \(\frac{27}{5}\) x \(\frac{1}{27}\) x \(\frac{5}{1}\) = 1 There is an explanation video available below. |
|
| 16. |
A crate of soft drinks contains 10 bottle of Coca-Cola 8 of Fanta and 6 of Sprite. If one bottle is selected at random, what is the probability that it is Not a Coca-Cola bottle? A. \(\frac{5}{12}\) B. \(\frac{1}{3}\) C. \(\frac{3}{4}\) D. \(\frac{7}{12}\) Detailed SolutionCoca-Cola = 10 bottles, Fanta = 8 bottles, Spirite = 6 bottlesTotal = 24 P(Coca-Cola) = \(\frac{10}{24}\); P(not Coca-Cola) 1 - \(\frac{10}{24}\) \(\frac{24 - 10}{24} = \frac{14}{24} = \frac{7}{12}\) There is an explanation video available below. |
|
| 17. |
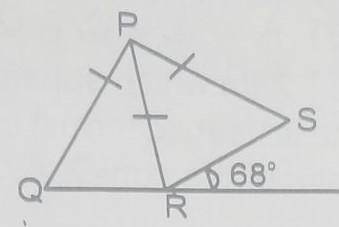 In this fiqure, PQ = PR = PS and SRT = 68\(^o\). Find QPS A. 136\(^o\) B. 124\(^o\) C. 112\(^o\) D. 68\(^o\) Detailed Solution
2y + 2x + QPS = 360\(^o\) i.e. (y + x) + QPS = 360\(^o\) QPS = 360\(^o\) - 2 (y + x) But x + y + 68\(^o\) = 180\(^o\) There; x + y = 180\(^o\) - 68\(^o\) = 112\(^o\) QPS = 360 - 2(112\(^o\)) = 360\(^o\) - 224 = 136\(^o\) There is an explanation video available below. |
|
| 18. |
Find the gradient of the line passing through the points (-2, 0) and (0, -4) A. 2 B. -4 C. -2 D. 4 Detailed SolutionGiven (-2, 0) ans (0, -4).Gradient = \(\frac{y_2 - y_1}{x_2 - x_1}\) = \(\frac{-4 - 0}{0 - (-2)}\) = \(\frac{-4}{2}\) = -2 There is an explanation video available below. |
|
| 19. |
Find the equation of the line through the points (5, 7) parallel to the line 7x + 5y = 12. A. 5x + 7y = 120 B. 7x + 5y = 70 C. x + y = 7 D. 15x + 17y = 90 Detailed SolutionEquation through (5,7) parallel to the line7x + 5y = 12 5y = 7x + 12 y = \(\frac{-7x}{5} + \frac{12}{5}\) Gradient = \(\frac{-7}{5}\) Required equation = \(\frac{y - 7}{x - 5} = \frac{-7}{5}\) i.e. 5y - 35 = -7x + 35 5y + 7x = 70 There is an explanation video available below. |
|
| 20. |
If N225.00 yields N27.00 in x years simple interest at the rate of 4% per annum, find x. A. 3 B. 4 C. 12 D. 17 Detailed SolutionPrincipal = N225.00, interest = N27.00Year = x, Rate = 4% 1 = \(\frac{PRT}{100}\) 27 = \(\frac{225 \times 4 \times x}{100}\) = 2700 = 900T T = \(\frac{2700}{900}\) = 3 years There is an explanation video available below. |
| 11. |
If log\(_{10}\)2 = 0.3010 and log\(_{10}\)3 = 0.4771, eventually without using the logarithm tables, log\(_{10}\)4.5 A. 0.3010 B. 0.4771 C. 0.6532 D. 0.9542 Detailed Solutionlog\(_{10}\)2 = 0.3010 and log\(_{10}\)3 = 04771log\(_{10} 4.5 = log_{10}\) (\(\frac{3 \times 3}{2}\)) log\(_{10}\) 3 + log\(_{10}\) 3 - log\(_{10}\)2 = 0.4471 + 0.771 - 0.3010 = 0.6532 There is an explanation video available below. |
|
| 12. |
Simplify \(\frac{324 - 4x^2}{2x + 18}\) A. 2(x - 9) B. 2(9 + x) C. 81 - x\(^2\) D. -2(x - 9) Detailed Solution234 - 4x\(^2\) = 18\(^2\) - (2x)\(^2\) = (18 - 2x)(18 + 2x)2x + 18 = 2x + 18 = (2x + 18) 18 - 2x = 2(a - x) or -2(x - a) There is an explanation video available below. |
|
| 13. |
In preparing rice cutlets, a cook used 75g of rice, 40g of margarine, 105g of meat and 20g of bread crumbs. Find the angle of the sector which represent meat in a pie chart? A. 30\(^o\) B. 60\(^o\) C. 112.5\(^o\) D. 157.5\(^o\) Detailed SolutionRice = 75g, Margarine = 40g, Meat = 105gBread = 20g Total = 240 Angle of sector represented by meat = \(\frac{105}{240} \times \frac{360^o}{1}\) = 157.5 There is an explanation video available below. |
|
| 14. |
The angle of a sector of a circle radius 10.5 cm is 48\(^o\). Calculate the perimeter of the sector. A. 25.4cm B. 25.4cm C. 25.6cm D. 29.8cm Detailed Solution
= \(\frac{48}{360}\) x 2\(\frac{22}{7}\) x 10.5 = \(\frac{48}{360}\) x 2\(\frac{22}{7}\) x \(\frac{21}{2}\) = \(\frac{4 \times 22 \times 3}{30} \times \frac{88}{10}\) = 8.8cm Perimeter = 8.8 + 2r = 8.8 + 2r = 8.8 + 2(10.5) = 8.8 + 21 = 29.8cm There is an explanation video available below. |
|
| 15. |
What is the product of \(\frac{27}{5}\), \((3)^{-3}\) and (\(\frac{1}{5})^{-1}\)? A. 5 B. 3 C. 1 D. \(\frac{1}{25}\) Detailed Solution\(\frac{27}{5} \times 3^{-3} \times \frac{(1)^{-1}}{5}\)= \(\frac{27}{5} \times \frac{1}{3^3} \times \frac{1}{\frac{1}{5}}\) \(\frac{27}{5}\) x \(\frac{1}{27}\) x \(\frac{5}{1}\) = 1 There is an explanation video available below. |
| 16. |
A crate of soft drinks contains 10 bottle of Coca-Cola 8 of Fanta and 6 of Sprite. If one bottle is selected at random, what is the probability that it is Not a Coca-Cola bottle? A. \(\frac{5}{12}\) B. \(\frac{1}{3}\) C. \(\frac{3}{4}\) D. \(\frac{7}{12}\) Detailed SolutionCoca-Cola = 10 bottles, Fanta = 8 bottles, Spirite = 6 bottlesTotal = 24 P(Coca-Cola) = \(\frac{10}{24}\); P(not Coca-Cola) 1 - \(\frac{10}{24}\) \(\frac{24 - 10}{24} = \frac{14}{24} = \frac{7}{12}\) There is an explanation video available below. |
|
| 17. |
 In this fiqure, PQ = PR = PS and SRT = 68\(^o\). Find QPS A. 136\(^o\) B. 124\(^o\) C. 112\(^o\) D. 68\(^o\) Detailed Solution
2y + 2x + QPS = 360\(^o\) i.e. (y + x) + QPS = 360\(^o\) QPS = 360\(^o\) - 2 (y + x) But x + y + 68\(^o\) = 180\(^o\) There; x + y = 180\(^o\) - 68\(^o\) = 112\(^o\) QPS = 360 - 2(112\(^o\)) = 360\(^o\) - 224 = 136\(^o\) There is an explanation video available below. |
|
| 18. |
Find the gradient of the line passing through the points (-2, 0) and (0, -4) A. 2 B. -4 C. -2 D. 4 Detailed SolutionGiven (-2, 0) ans (0, -4).Gradient = \(\frac{y_2 - y_1}{x_2 - x_1}\) = \(\frac{-4 - 0}{0 - (-2)}\) = \(\frac{-4}{2}\) = -2 There is an explanation video available below. |
|
| 19. |
Find the equation of the line through the points (5, 7) parallel to the line 7x + 5y = 12. A. 5x + 7y = 120 B. 7x + 5y = 70 C. x + y = 7 D. 15x + 17y = 90 Detailed SolutionEquation through (5,7) parallel to the line7x + 5y = 12 5y = 7x + 12 y = \(\frac{-7x}{5} + \frac{12}{5}\) Gradient = \(\frac{-7}{5}\) Required equation = \(\frac{y - 7}{x - 5} = \frac{-7}{5}\) i.e. 5y - 35 = -7x + 35 5y + 7x = 70 There is an explanation video available below. |
|
| 20. |
If N225.00 yields N27.00 in x years simple interest at the rate of 4% per annum, find x. A. 3 B. 4 C. 12 D. 17 Detailed SolutionPrincipal = N225.00, interest = N27.00Year = x, Rate = 4% 1 = \(\frac{PRT}{100}\) 27 = \(\frac{225 \times 4 \times x}{100}\) = 2700 = 900T T = \(\frac{2700}{900}\) = 3 years There is an explanation video available below. |