Year :
2009
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
31 - 40 of 50 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
What is the value of r if the distance between the point (4,2) and (1,r) is 3 units? A. 1 B. 2 C. 3 D. 4 Detailed SolutionA(4,2) and B(1,r), AB = 3 units3 = √ (x2- x1)2 + (y2-y1)2 3 = √ (4-1)2 + (2-r)2 3 = √ 32 + (2-r)2 3 = √ 9 + 4 – 4r + r2 3 = √ r2 - 4r + 13 9 = r2 - 4r + 13 By squaring both sides r2 - 4r + 4 = 0 (r-2)(r-2) = 0 r = 2 There is an explanation video available below. |
|
| 32. |
If y = 3 cos 4x, dy/dx equals? A. 6 sin 8x B. -24 sin 4x C. 12 sin 4x D. -12 sin 4x Detailed Solutiony = 3 cos 4xApplying product rule: \(\frac{dy}{dx}\) = u\(\frac{dv}{dx}\) + v\(\frac{du}{dx}\) Where u = 3 and v = cos 4x \(\frac{du}{dx}\) of 3 = 0 and \(\frac{dv}{dx}\) of cos 4x = -4sin 4x \(\frac{dy}{dx}\) = 3 \(\times\) -4 sin 4x + cos 4x \(\times\) 0 \(\frac{dy}{dx}\) = -12 sin 4x There is an explanation video available below. |
|
| 33. |
Find the value of sin 45° - cos 30° A. \(\frac{2+\sqrt{3}}{4}\) B. \(\frac{\sqrt{2}+\sqrt{3}}{4}\) C. \(\frac{\sqrt{2}+\sqrt{3}}{2}\) D. \(\frac{\sqrt{2}-\sqrt{3}}{2}\) Detailed Solution\(Sin 45 - cos 30\\\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}\\ =\frac{\sqrt{2}-\sqrt{3}}{2}\) There is an explanation video available below. |
|
| 34. |
A cliff on the bank of a river is 300 meter high. if the angle of depression of a point on the opposite side of the river is 60º, find the width of the river? A. 100m B. 75√3 m C. 100√3m D. 200√3m |
|
| 35. |
If s = (2 + 3t)(5t - 4), find ds/dt when t = 4/5 secs A. 0 units per sec B. 15 units per sec C. 22 unit per sec D. 26 units per sec Detailed Solutionx = (2+3t)(5t-4)Let u = 2+3t ∴du/dt = 3 and v = 5t-4 ∴dv/dt = 5 dx/dt = Vdu/dt + Udv/dt = (5t-4)3 + (2+3t)5 = 15t - 12 + 10 + 15t = 30t - 2 = 30x4/5 - 2 = 24 - 2 = 22 There is an explanation video available below. |
|
| 36. |
The distance traveled by a particle from a fixed point is given as s = (t\(^3\) - t\(^2\) - t + 5)cm. Find the minimum distance that the particle can cover from the fixed point? A. 2.3 cm B. 4.0 cm C. 5.2 cm D. 6.0 cm Detailed SolutionS = t\(^3\) - t\(^2\) - t + 5ds/dt = 3t\(^2\) - 2t - 1 As ds = 0 3t\(^2\) - 2t - 1 = 0 (3t+1)(t-1) = 0 ∴ t = 1 or -1/3 At min pt t = 1 S = t\(^3\) - t\(^2\) - t + 5 put t = 1 = 1\(^3\) - \1(^2\) - 1 + 5 = 1 - 1 - 1 + 5 = 4 There is an explanation video available below. |
|
| 37. |
Evaluate ∫sec\(^2\)θ dθ? A. sec θ tan θ + k B. tan θ + k C. 2sec θ + k D. sec θ + k Detailed Solution∫sec2θ dθ = ∫ 1/cos2 dθ∫(cos)-2 dθ, let u = cos θ ∴∫u-2 = 1/u + c ∫cos θ = sin θ + c ∫sec-2θ = 1/u sin θ + c = (sinθ / cosθ) + c = Tan θ + c There is an explanation video available below. |
|
| 38. |
 Table: A. 180 B. 120 C. 110 D. 40 Detailed Solution20 + 2x + 60 + 40 + x + 50 = 260170 + 3x = 260 3x = 260 - 170 3x = 90 x = 90/3 = 30 At least 4 days 4 days = 40 5 days = 30 6 days = 50 Total = 120 There is an explanation video available below. |
|
| 39. |
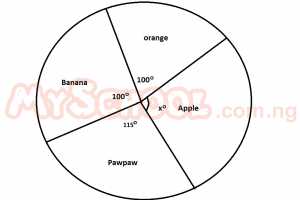 The pie chart above represents 400 fruits on display in a grocery store. How many apples are in the store? A. 45 B. 50 C. 60 D. 75 Detailed SolutionSectorial angle of apple100 + 100 + 115 + x = 30o 315 + x = 360 x = 360 - 315 x = 45o 360o represents 400 1o represents 400 / 360 45o represents (400/360) x (45/1) = 50 apples There is an explanation video available below. |
|
| 40. |
The probability of a student passing any examination is 2/3. If the students takes three examination, what is the probability that he will not pass any of them? A. 2/3 B. 4/9 C. 8/27 D. 1/27 Detailed SolutionP(pass) = 2/3P(not pass) = 1 - 2/3 = 1/3 P(not passing any of the 3 Exams) = 1/3 x 1/3 x 1/3 = 1/27 There is an explanation video available below. |
| 31. |
What is the value of r if the distance between the point (4,2) and (1,r) is 3 units? A. 1 B. 2 C. 3 D. 4 Detailed SolutionA(4,2) and B(1,r), AB = 3 units3 = √ (x2- x1)2 + (y2-y1)2 3 = √ (4-1)2 + (2-r)2 3 = √ 32 + (2-r)2 3 = √ 9 + 4 – 4r + r2 3 = √ r2 - 4r + 13 9 = r2 - 4r + 13 By squaring both sides r2 - 4r + 4 = 0 (r-2)(r-2) = 0 r = 2 There is an explanation video available below. |
|
| 32. |
If y = 3 cos 4x, dy/dx equals? A. 6 sin 8x B. -24 sin 4x C. 12 sin 4x D. -12 sin 4x Detailed Solutiony = 3 cos 4xApplying product rule: \(\frac{dy}{dx}\) = u\(\frac{dv}{dx}\) + v\(\frac{du}{dx}\) Where u = 3 and v = cos 4x \(\frac{du}{dx}\) of 3 = 0 and \(\frac{dv}{dx}\) of cos 4x = -4sin 4x \(\frac{dy}{dx}\) = 3 \(\times\) -4 sin 4x + cos 4x \(\times\) 0 \(\frac{dy}{dx}\) = -12 sin 4x There is an explanation video available below. |
|
| 33. |
Find the value of sin 45° - cos 30° A. \(\frac{2+\sqrt{3}}{4}\) B. \(\frac{\sqrt{2}+\sqrt{3}}{4}\) C. \(\frac{\sqrt{2}+\sqrt{3}}{2}\) D. \(\frac{\sqrt{2}-\sqrt{3}}{2}\) Detailed Solution\(Sin 45 - cos 30\\\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}\\ =\frac{\sqrt{2}-\sqrt{3}}{2}\) There is an explanation video available below. |
|
| 34. |
A cliff on the bank of a river is 300 meter high. if the angle of depression of a point on the opposite side of the river is 60º, find the width of the river? A. 100m B. 75√3 m C. 100√3m D. 200√3m |
|
| 35. |
If s = (2 + 3t)(5t - 4), find ds/dt when t = 4/5 secs A. 0 units per sec B. 15 units per sec C. 22 unit per sec D. 26 units per sec Detailed Solutionx = (2+3t)(5t-4)Let u = 2+3t ∴du/dt = 3 and v = 5t-4 ∴dv/dt = 5 dx/dt = Vdu/dt + Udv/dt = (5t-4)3 + (2+3t)5 = 15t - 12 + 10 + 15t = 30t - 2 = 30x4/5 - 2 = 24 - 2 = 22 There is an explanation video available below. |
| 36. |
The distance traveled by a particle from a fixed point is given as s = (t\(^3\) - t\(^2\) - t + 5)cm. Find the minimum distance that the particle can cover from the fixed point? A. 2.3 cm B. 4.0 cm C. 5.2 cm D. 6.0 cm Detailed SolutionS = t\(^3\) - t\(^2\) - t + 5ds/dt = 3t\(^2\) - 2t - 1 As ds = 0 3t\(^2\) - 2t - 1 = 0 (3t+1)(t-1) = 0 ∴ t = 1 or -1/3 At min pt t = 1 S = t\(^3\) - t\(^2\) - t + 5 put t = 1 = 1\(^3\) - \1(^2\) - 1 + 5 = 1 - 1 - 1 + 5 = 4 There is an explanation video available below. |
|
| 37. |
Evaluate ∫sec\(^2\)θ dθ? A. sec θ tan θ + k B. tan θ + k C. 2sec θ + k D. sec θ + k Detailed Solution∫sec2θ dθ = ∫ 1/cos2 dθ∫(cos)-2 dθ, let u = cos θ ∴∫u-2 = 1/u + c ∫cos θ = sin θ + c ∫sec-2θ = 1/u sin θ + c = (sinθ / cosθ) + c = Tan θ + c There is an explanation video available below. |
|
| 38. |
 Table: A. 180 B. 120 C. 110 D. 40 Detailed Solution20 + 2x + 60 + 40 + x + 50 = 260170 + 3x = 260 3x = 260 - 170 3x = 90 x = 90/3 = 30 At least 4 days 4 days = 40 5 days = 30 6 days = 50 Total = 120 There is an explanation video available below. |
|
| 39. |
 The pie chart above represents 400 fruits on display in a grocery store. How many apples are in the store? A. 45 B. 50 C. 60 D. 75 Detailed SolutionSectorial angle of apple100 + 100 + 115 + x = 30o 315 + x = 360 x = 360 - 315 x = 45o 360o represents 400 1o represents 400 / 360 45o represents (400/360) x (45/1) = 50 apples There is an explanation video available below. |
|
| 40. |
The probability of a student passing any examination is 2/3. If the students takes three examination, what is the probability that he will not pass any of them? A. 2/3 B. 4/9 C. 8/27 D. 1/27 Detailed SolutionP(pass) = 2/3P(not pass) = 1 - 2/3 = 1/3 P(not passing any of the 3 Exams) = 1/3 x 1/3 x 1/3 = 1/27 There is an explanation video available below. |