Year :
2021
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
41 - 49 of 49 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
\(\overline{XY}\) is a line segments with the coordinates X (- 8,- 12) and Y(p,q). if the midpoint of \(\overline{XY}\) is (-4,-2) find the coordinates of Y. A. (-6,-2) B. (0,8) C. (4,10) D. (0,4) Detailed SolutionThe formula for midpoint = \(\frac{x_1 + x_2}{2}\), \(\frac{y_1 + y_2}{2}\)(-4,-2) = (x,y) x = \(\frac{x_1 + x_2}{2}\) -4 = \(\frac{-8 + p}{2}\) -4 * 2 = -8 + p -8 + 8 = p : p = 0 y = \(\frac{y_1 + y_2}{2}\) -2 = \(\frac{-12 + q}{2}\) -2 * 2 = -12 + q -4 + 12 = q : q = 8 |
|
| 42. |
500 tickets were sold for a concert tickets for adults and children were sold at $4.50 and $3.00 respectively if the total receipts for the concerts was $1987.50 how many tickets for adults were sold? A. 325 B. 235 C. 175 D. 400 Detailed SolutionA for AdultsC for children a + c = 500 c = 500 - a 4.5a + 3c = 1987.50 where c = 500 - a 4.5a + 3(500 - a) = 1987.50 4.5a - 3a = 1987.50 - 1500 1.5a = 487.5 a = 487.5 / 1.5 a = 325 tickets c = 500 - a c = 500 - 325 c = 175 tickets Check: from 4.5a + 3c 4.5 (325) = 1,462.5 + 3(175) = 525 |
|
| 43. |
The distance d between two villages east more than 18 KM but not more than 23KM.which of these inequalities represents the statements? A. 18 ≤ d ≤ 23 B. 18 < d < 23 C. 18 ≤ d < 23 D. 18 < d ≤ 23 Detailed Solutiondistance d more than 18 KM = d > 18 0r 18 < ddistance d but not more than 23 KM = d ≤ 23 Mathematically; 18 < d ≤ 23 |
|
| 44. |
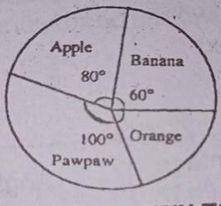 The pie chart represents the distribution of fruits on display in the shop if there are 60 apples on display how many oranges are there? A. 80 B. 270 C. 120 D. 90 Detailed SolutionTotal angles = 360°100 + 60 + 80 + M = 360 M = 360 - 240 = 120 Orange (M) = 120° and F ( fruits in total) For Apples: \(\frac{80}{360} \times F\) = 60 F = \(\frac{60 \times 360}{80}\) F = 270 fruits in total For Orange = \(\frac{120}{360} \times 270\) = 90 oranges |
|
| 45. |
A box contains 40 identical balls of which 10 are red and 12 are blue. if a ball is selected at random from the box what is the probability that it is neither red nor blue? A. \(\frac{9}{20}\) B. \(\frac{3}{10}\) C. \(\frac{1}{4}\) D. \(\frac{11}{20}\) Detailed SolutionTotal number = 40number of red = 10 Pr (R) = \(\frac{10}{40}\) Pr(blue) = \(\frac{12}{40}\) probability (neither red nor blue) = 1 - \(\frac{10}{40}\) - \(\frac{12}{40}\) = \(\frac{40 -12 -10}{40}\) = \(\frac{18}{40}\) or \(\frac{9}{20}\) |
|
| 46. |
A fair die is tossed twice what is the probability of get a sum of at least 10. A. \(\frac{5}{36}\) B. \(\frac{2}{3}\) C. \(\frac{5}{18}\) D. \(\frac{1}{6\) Detailed Solution\(\begin{array}{c|c}& 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 1,1 & 1,2 & 1,3 & 1,4 & 1,5 & 1,6 \\ \hline 2 & 2,1 & 2,2 & 2,3 & 2,4 & 2,5 & 2,6 \\ \hline 3 & 3,1 & 3,2 & 3,3 & 3,4 & 3,5 & 3,6 \\ \hline 4 & 4,1 & 4,2 & 4,3 & 4,4 & 4,5 & 4,6 \\ 5 & 5,1 & 5,2 & 5,3 & 5,4 & 5,5 & 5,6 \\ \hline 6 & 6,1 & 6,2 & 6,3 & 6,4 & 6,5 & 6,6\end{array}\) From the table |
|
| 47. |
A man will be (x+10)years old in 8years time. If 2years ago he was 63 years., find the value of x A. 55 B. 63 C. 57 D. 67 Detailed SolutionA man will be (x+10) years old in 8years time.As at today, he is x + 2 years of age. The man was 63 years old 2 years ago, so he is 63+2=65 now. 8 years from now, he will be 65+8=73. He will be (x+10) years old when he is 73. So x+10=73 x=73-10=63 |
|
| 48. |
The equation of a line is given as 3 x - 5y = 7. Find its gradient (slope) A. \(\frac{5}{3}\). B. \(\frac{3}{5}\). C. \(\frac{-3}{5}\). D. \(\frac{-5}{3}\). Detailed Solutionthe form y=mx+cwhere m is the gradient and c is the y-intercept. the equation to gives 5y=-3x+7. comparing this with the general equation y=mx+c, you can see that m= the gradient= \(\frac{-3}{5}\). |
|
| 49. |
For what value of x is \(\frac{4 - 2x}{x + 1}\) undefined. A. 2 B. -1 C. 1 D. -2 Detailed SolutionA rational expression is undefined when the denominator is equal to zero.when x = -1 The denominator in this equation : x + 1 --> -1 + 1 = 0 This expression is undefined when x = -1 |
| 41. |
\(\overline{XY}\) is a line segments with the coordinates X (- 8,- 12) and Y(p,q). if the midpoint of \(\overline{XY}\) is (-4,-2) find the coordinates of Y. A. (-6,-2) B. (0,8) C. (4,10) D. (0,4) Detailed SolutionThe formula for midpoint = \(\frac{x_1 + x_2}{2}\), \(\frac{y_1 + y_2}{2}\)(-4,-2) = (x,y) x = \(\frac{x_1 + x_2}{2}\) -4 = \(\frac{-8 + p}{2}\) -4 * 2 = -8 + p -8 + 8 = p : p = 0 y = \(\frac{y_1 + y_2}{2}\) -2 = \(\frac{-12 + q}{2}\) -2 * 2 = -12 + q -4 + 12 = q : q = 8 |
|
| 42. |
500 tickets were sold for a concert tickets for adults and children were sold at $4.50 and $3.00 respectively if the total receipts for the concerts was $1987.50 how many tickets for adults were sold? A. 325 B. 235 C. 175 D. 400 Detailed SolutionA for AdultsC for children a + c = 500 c = 500 - a 4.5a + 3c = 1987.50 where c = 500 - a 4.5a + 3(500 - a) = 1987.50 4.5a - 3a = 1987.50 - 1500 1.5a = 487.5 a = 487.5 / 1.5 a = 325 tickets c = 500 - a c = 500 - 325 c = 175 tickets Check: from 4.5a + 3c 4.5 (325) = 1,462.5 + 3(175) = 525 |
|
| 43. |
The distance d between two villages east more than 18 KM but not more than 23KM.which of these inequalities represents the statements? A. 18 ≤ d ≤ 23 B. 18 < d < 23 C. 18 ≤ d < 23 D. 18 < d ≤ 23 Detailed Solutiondistance d more than 18 KM = d > 18 0r 18 < ddistance d but not more than 23 KM = d ≤ 23 Mathematically; 18 < d ≤ 23 |
|
| 44. |
 The pie chart represents the distribution of fruits on display in the shop if there are 60 apples on display how many oranges are there? A. 80 B. 270 C. 120 D. 90 Detailed SolutionTotal angles = 360°100 + 60 + 80 + M = 360 M = 360 - 240 = 120 Orange (M) = 120° and F ( fruits in total) For Apples: \(\frac{80}{360} \times F\) = 60 F = \(\frac{60 \times 360}{80}\) F = 270 fruits in total For Orange = \(\frac{120}{360} \times 270\) = 90 oranges |
|
| 45. |
A box contains 40 identical balls of which 10 are red and 12 are blue. if a ball is selected at random from the box what is the probability that it is neither red nor blue? A. \(\frac{9}{20}\) B. \(\frac{3}{10}\) C. \(\frac{1}{4}\) D. \(\frac{11}{20}\) Detailed SolutionTotal number = 40number of red = 10 Pr (R) = \(\frac{10}{40}\) Pr(blue) = \(\frac{12}{40}\) probability (neither red nor blue) = 1 - \(\frac{10}{40}\) - \(\frac{12}{40}\) = \(\frac{40 -12 -10}{40}\) = \(\frac{18}{40}\) or \(\frac{9}{20}\) |
| 46. |
A fair die is tossed twice what is the probability of get a sum of at least 10. A. \(\frac{5}{36}\) B. \(\frac{2}{3}\) C. \(\frac{5}{18}\) D. \(\frac{1}{6\) Detailed Solution\(\begin{array}{c|c}& 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 1,1 & 1,2 & 1,3 & 1,4 & 1,5 & 1,6 \\ \hline 2 & 2,1 & 2,2 & 2,3 & 2,4 & 2,5 & 2,6 \\ \hline 3 & 3,1 & 3,2 & 3,3 & 3,4 & 3,5 & 3,6 \\ \hline 4 & 4,1 & 4,2 & 4,3 & 4,4 & 4,5 & 4,6 \\ 5 & 5,1 & 5,2 & 5,3 & 5,4 & 5,5 & 5,6 \\ \hline 6 & 6,1 & 6,2 & 6,3 & 6,4 & 6,5 & 6,6\end{array}\) From the table |
|
| 47. |
A man will be (x+10)years old in 8years time. If 2years ago he was 63 years., find the value of x A. 55 B. 63 C. 57 D. 67 Detailed SolutionA man will be (x+10) years old in 8years time.As at today, he is x + 2 years of age. The man was 63 years old 2 years ago, so he is 63+2=65 now. 8 years from now, he will be 65+8=73. He will be (x+10) years old when he is 73. So x+10=73 x=73-10=63 |
|
| 48. |
The equation of a line is given as 3 x - 5y = 7. Find its gradient (slope) A. \(\frac{5}{3}\). B. \(\frac{3}{5}\). C. \(\frac{-3}{5}\). D. \(\frac{-5}{3}\). Detailed Solutionthe form y=mx+cwhere m is the gradient and c is the y-intercept. the equation to gives 5y=-3x+7. comparing this with the general equation y=mx+c, you can see that m= the gradient= \(\frac{-3}{5}\). |
|
| 49. |
For what value of x is \(\frac{4 - 2x}{x + 1}\) undefined. A. 2 B. -1 C. 1 D. -2 Detailed SolutionA rational expression is undefined when the denominator is equal to zero.when x = -1 The denominator in this equation : x + 1 --> -1 + 1 = 0 This expression is undefined when x = -1 |