Year :
2002
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 48 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
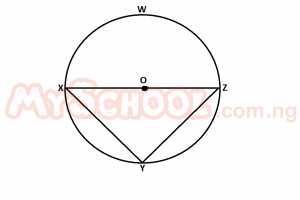 In the diagram above , XZ is the diameter of the circle XZW, with center O and radius 15/2 cm. If XY = 12 cm, find the area of the triangle XYZ A. 54 cm2 B. 45 cm2 C. 27 cm2 D. 75 cm2 Detailed Solutionsince radius = 15/2 diameter = 2 * (15/2) = 15cm XYZ is a right angled triangle ∴ 152 = 122 + (YZ)2 225 = 144 = (YZ)2 225 - 144 = (YZ)2 81 = (YZ)2 √81 = YZ 9 = YZ Area of ΔXYZ = 1/2bh (1/2) * 9 * 12 9 * 6 = 54 = 54cm2 |
|
| 42. |
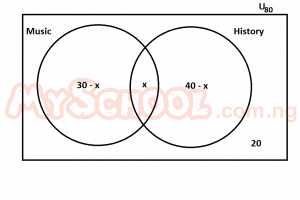 The venn diagram above shows the numbers of students offering music and history in a class of 80 students. If a student is picked at random from the class, what is the probability that he offers Music only? A. 0.38 B. 0.13 C. 0.50 D. 0.25 Detailed Solution30 - x + x + 40 - x = 80 - 2070 - x = 60 - x = 60 - 70 - x = - 10 ∴ x = 10 Music only = 30 - x = 30 - 10 20 P(music only) = 20/80 = 1/4 = 0.25 |
|
| 43. |
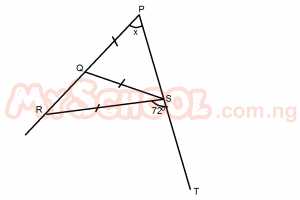
 In the diagram above, PST is a straight line, PQ = QS = RS. If ∠RST = 72o, find x A. 36o B. 18o C. 72o D. 24o Detailed Solution
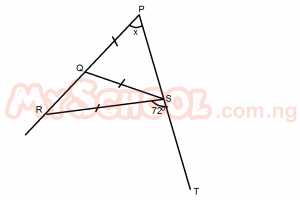 In Δ QRS, ∠RQS = ∠PSQ + X(Extr ∠ = sum of two intr. opp ∠s) ∴ ∠RQS = X + X = 2X Also ∠QRS = 2X(base ∠s of isoc Δ QRS in Δ PRS, 72 = ∠RPS + ∠PRS(Extr, ∠ = sum of two intr. opp ∠s) ∴ 72 = x + 2x 72 = 3x x = 72/3 x = 24o |
|
| 44. |
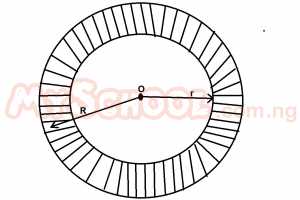 In the diagram above are two concentric circles of radii r and R respectively with center O. If r = 2/3R, express the area of the shaded portion in terms of π and R A. 21/25πR2 B. 9/25πR2 C. 21/23πR2 D. 5/9πR2 Detailed Solutionr = \(\frac{2}{3}\)R∴R = \(\frac{3}{3}\)R Area of small circle = πr2 = π(\(\frac{2R}{3}\))2 Area of the big circle πr2 = π\(\frac{(3R)^2}{3}\) Area of shaded portion = π(\(\frac{3R}{3}\))2 - π(\(\frac{2R}{3}\))2 = π[(\(\frac{3R}{3}\))2 - (\(\frac{2R}{3}\))2] = π[(\(\frac{3R}{3}) + (\frac{2R}{3}) - (\frac{3R}{3}\)) - (\(\frac{2R}{3}\))] = π[(\(\frac{5R}{3}\)) (\(\frac{R}{3}\))] = π x \(\frac{5R |
|
| 45. |
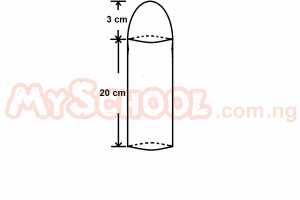 In the diagram above, a cylinder is summounted by a hemisphere bowl. Calculate the volume of the solid. A. 180 πcm3 B. 162 πcm3 C. 216 πcm3 D. 198 πcm3 Detailed SolutionVolume of cylinder = πr2h= π x 32 x 20 = π x 9 x 20 = 180 πcm3 Volume of hemisphere = 2/3πr3 = 2/3 x π x 32 = 2 x π x 32 = 2 x π x 9 = 18π = Volume of the solid = 180π x 18π = 198πcm3 |
|
| 46. |
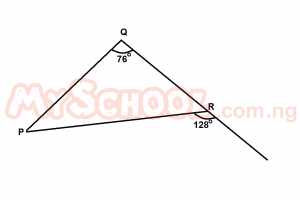
 The triangle PQR above is A. an obtuse-angled triangle B. a scalene triangle C. an isosceles triangle D. an equilateral triangle Detailed Solution
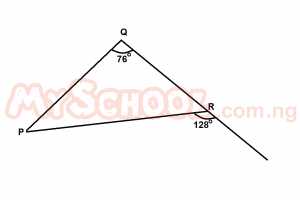 = 52o ∠QPR + 76 + 52 = 180(extr ∠ = sum of intr. opp ∠s) ∠QPR + 128 = 180 ∠QPR = 180 - 128 = 52o ∴ΔPQR is an isosceles triangle |
|
| 47. |
 Table: A. 210 B. 40 C. 120 D. 160 Detailed Solution20 + X + 50 + 40 + 2X + 60 = 2603X + 170 = 260 3X = 260 - 170 3x = 90 x = 30 Absent for at least 4 days i.e 40 + 2x + 60 = 40 + (2 x 30) + 60 = 40 + 60 + 60 = 160 |
|
| 48. |
Using the graph find the values of p and q if px + qy \(\geq\) 4 A. p = 2, q = -1 B. p = -1, q = 2 C. p = 2, q = 2 D. p = 1, q = 2 Detailed Solutionm = \(\frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 0}{0 - (4)} = \frac{2}{4} = \frac{1}{2}\)\(\frac{y_2 - y_1}{x_2 - x_1} \geq m\) \(\frac{y - 0}{x + 4} \geq \frac{1}{2}\) 2y \(\geq\) x + 4, -x + 2y \(\geq\) 4 = px + qy \(\geq\) 4 p = -1, q = 2 |
| 41. |
 In the diagram above , XZ is the diameter of the circle XZW, with center O and radius 15/2 cm. If XY = 12 cm, find the area of the triangle XYZ A. 54 cm2 B. 45 cm2 C. 27 cm2 D. 75 cm2 Detailed Solutionsince radius = 15/2 diameter = 2 * (15/2) = 15cm XYZ is a right angled triangle ∴ 152 = 122 + (YZ)2 225 = 144 = (YZ)2 225 - 144 = (YZ)2 81 = (YZ)2 √81 = YZ 9 = YZ Area of ΔXYZ = 1/2bh (1/2) * 9 * 12 9 * 6 = 54 = 54cm2 |
|
| 42. |
 The venn diagram above shows the numbers of students offering music and history in a class of 80 students. If a student is picked at random from the class, what is the probability that he offers Music only? A. 0.38 B. 0.13 C. 0.50 D. 0.25 Detailed Solution30 - x + x + 40 - x = 80 - 2070 - x = 60 - x = 60 - 70 - x = - 10 ∴ x = 10 Music only = 30 - x = 30 - 10 20 P(music only) = 20/80 = 1/4 = 0.25 |
|
| 43. |
 In the diagram above, PST is a straight line, PQ = QS = RS. If ∠RST = 72o, find x A. 36o B. 18o C. 72o D. 24o Detailed Solution
 In Δ QRS, ∠RQS = ∠PSQ + X(Extr ∠ = sum of two intr. opp ∠s) ∴ ∠RQS = X + X = 2X Also ∠QRS = 2X(base ∠s of isoc Δ QRS in Δ PRS, 72 = ∠RPS + ∠PRS(Extr, ∠ = sum of two intr. opp ∠s) ∴ 72 = x + 2x 72 = 3x x = 72/3 x = 24o |
|
| 44. |
 In the diagram above are two concentric circles of radii r and R respectively with center O. If r = 2/3R, express the area of the shaded portion in terms of π and R A. 21/25πR2 B. 9/25πR2 C. 21/23πR2 D. 5/9πR2 Detailed Solutionr = \(\frac{2}{3}\)R∴R = \(\frac{3}{3}\)R Area of small circle = πr2 = π(\(\frac{2R}{3}\))2 Area of the big circle πr2 = π\(\frac{(3R)^2}{3}\) Area of shaded portion = π(\(\frac{3R}{3}\))2 - π(\(\frac{2R}{3}\))2 = π[(\(\frac{3R}{3}\))2 - (\(\frac{2R}{3}\))2] = π[(\(\frac{3R}{3}) + (\frac{2R}{3}) - (\frac{3R}{3}\)) - (\(\frac{2R}{3}\))] = π[(\(\frac{5R}{3}\)) (\(\frac{R}{3}\))] = π x \(\frac{5R |
| 45. |
 In the diagram above, a cylinder is summounted by a hemisphere bowl. Calculate the volume of the solid. A. 180 πcm3 B. 162 πcm3 C. 216 πcm3 D. 198 πcm3 Detailed SolutionVolume of cylinder = πr2h= π x 32 x 20 = π x 9 x 20 = 180 πcm3 Volume of hemisphere = 2/3πr3 = 2/3 x π x 32 = 2 x π x 32 = 2 x π x 9 = 18π = Volume of the solid = 180π x 18π = 198πcm3 |
|
| 46. |
 The triangle PQR above is A. an obtuse-angled triangle B. a scalene triangle C. an isosceles triangle D. an equilateral triangle Detailed Solution
 = 52o ∠QPR + 76 + 52 = 180(extr ∠ = sum of intr. opp ∠s) ∠QPR + 128 = 180 ∠QPR = 180 - 128 = 52o ∴ΔPQR is an isosceles triangle |
|
| 47. |
 Table: A. 210 B. 40 C. 120 D. 160 Detailed Solution20 + X + 50 + 40 + 2X + 60 = 2603X + 170 = 260 3X = 260 - 170 3x = 90 x = 30 Absent for at least 4 days i.e 40 + 2x + 60 = 40 + (2 x 30) + 60 = 40 + 60 + 60 = 160 |
|
| 48. |
Using the graph find the values of p and q if px + qy \(\geq\) 4 A. p = 2, q = -1 B. p = -1, q = 2 C. p = 2, q = 2 D. p = 1, q = 2 Detailed Solutionm = \(\frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 0}{0 - (4)} = \frac{2}{4} = \frac{1}{2}\)\(\frac{y_2 - y_1}{x_2 - x_1} \geq m\) \(\frac{y - 0}{x + 4} \geq \frac{1}{2}\) 2y \(\geq\) x + 4, -x + 2y \(\geq\) 4 = px + qy \(\geq\) 4 p = -1, q = 2 |