Year :
1978
Title :
Mathematics (Core)
Exam :
JAMB Exam
Paper 1 | Objectives
41 - 48 of 48 Questions
| # | Question | Ans |
|---|---|---|
| 41. |
The angle of elevation of the top of a vertical tower from a point A on the ground is 60o. From a point B, 2 units of distance further away from the foot of the tower, the angle of elevation of the tower is 45o. Find the distance of A from the foot of the tower A. 3 + \(\sqrt{3}\) B. 5 + \(\sqrt{3}\) C. 3 - \(\sqrt{3}\) D. 1 E. \(\sqrt{3}\) - 1 |
D |
| 42. |
The vectors a and b are given in terms of two perpendicular units vectors i and j on a plane by a = 2i - 3j, b = -i + 2j. Find the magnitude of the vector a + 3b A. 2 B. 4 C. \(\sqrt{10}\) D. 35 E. 2.2 Detailed Solutiona = 2i - 3j - 3i + 6j= -i + 3j = \(\sqrt{5 \times 2}\) = \(\sqrt{10}\) |
|
| 43. |
Add the same number to the numerator and denominator of \(\frac{3}{18}\). If the resulting fraction is \(\frac{1}{2}\), then the number added is A. 13 B. 14 C. 15 D. 12 E. 11 Detailed SolutionLet x be the no. \(\frac{3 + x}{ |
|
| 44. |
The smallest number such that when it is divided by 8 has a remainder of 6 and when it is divided by 9, has a remainder of 7 is A. 387 B. 493 C. 502 D. 441 E. 634 Detailed SolutionPossible multiples of 8 and 9 = 72, 144, 216, 288, 360, 432, 576, 648.\(\frac{387}{8}\) has remainder = 3; \(\frac{387}{9}\) has remainder 0. \(\frac{493}{8}\) has remainder 5; \(\frac{493}{9}\) has remainder 7. \(\frac{502}{8}\) has remainder 6; \(\frac{502}{9}\) has remainder 7. \(\frac{441}{8}\) has remainder 1; \(\frac{441}{9}\) has remainder 0. \(\frac{634}{8}\) has remainder 2; \(\frac{634}{9}\) has remainder 4. Hence 502 is the answer. |
|
| 45. |
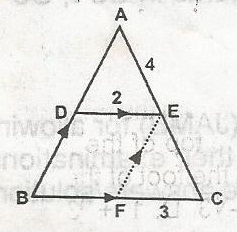 In the figure, DE//BC: DB//FE: DE = 2cm, FC = 3cm, AE = 4cm. Determine the length of EC. A. 4cm B. 6cm C. 3cm D. 2cm E. 1cm Detailed SolutionAngles ADE and EFC are similar,Therefore, = \(\frac{x}{3} = \frac{4}{2}\) = \(\frac{x}{3} = 2\) x = 3 x 2 = 6 |
|
| 46. |
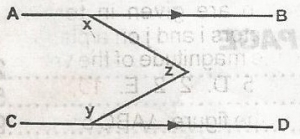 In the figure, AB is parallel to CD then x + y + z is A. 185o B. 200o C. 270o D. 360o E. 195o Detailed Solutionx + y + z = 360o |
|
| 47. |
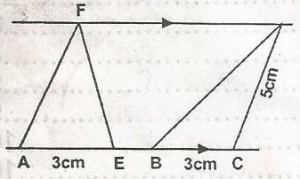 In the Figure FD\\AC, the area of AEF = 6sq.cm. AE = 3cm, BC = 3cm, CD = 5cm, < BCD is an obtuse angle. Find the length of BD. A. \(\sqrt{33}\) B. 6 C. 4 D. 2\(\sqrt{13}\) E. 4\(\sqrt{5}\) Detailed SolutionArea of triangle AEF = 6sq. cmarea of triangle = \(\frac{1}{2}\)bh (Line DX makes right angles with the parallel lines) 6 = \(\frac{1}{2}\) x 3 x h 6 = 3h 3h = \(\frac{12}{3}\) h = 4 = DX From D, C x D, CX2 = 52 - 42 = 25 - 16 = 9 Cx = 3. From angle B x D, Bx = 6(i.e. 3 + 3) BD2 = 42 + 62 = 16 + 36 = 52 BD = \(\sqrt{4 \times 13}\) |
|
| 48. |
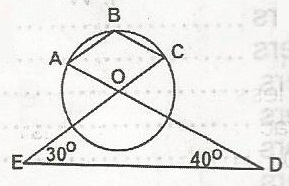 In the figure, 0 is the centre of the circle ABC, < CED = 30o, < EDA = 40o. What is the size of < ABC? A. 70o B. 110o C. 130o D. 125o E. 145o Detailed SolutionIf < CED = 30o, and < EDA = 40o then < ABC = 125o |
| 41. |
The angle of elevation of the top of a vertical tower from a point A on the ground is 60o. From a point B, 2 units of distance further away from the foot of the tower, the angle of elevation of the tower is 45o. Find the distance of A from the foot of the tower A. 3 + \(\sqrt{3}\) B. 5 + \(\sqrt{3}\) C. 3 - \(\sqrt{3}\) D. 1 E. \(\sqrt{3}\) - 1 |
D |
| 42. |
The vectors a and b are given in terms of two perpendicular units vectors i and j on a plane by a = 2i - 3j, b = -i + 2j. Find the magnitude of the vector a + 3b A. 2 B. 4 C. \(\sqrt{10}\) D. 35 E. 2.2 Detailed Solutiona = 2i - 3j - 3i + 6j= -i + 3j = \(\sqrt{5 \times 2}\) = \(\sqrt{10}\) |
|
| 43. |
Add the same number to the numerator and denominator of \(\frac{3}{18}\). If the resulting fraction is \(\frac{1}{2}\), then the number added is A. 13 B. 14 C. 15 D. 12 E. 11 Detailed SolutionLet x be the no. \(\frac{3 + x}{ |
|
| 44. |
The smallest number such that when it is divided by 8 has a remainder of 6 and when it is divided by 9, has a remainder of 7 is A. 387 B. 493 C. 502 D. 441 E. 634 Detailed SolutionPossible multiples of 8 and 9 = 72, 144, 216, 288, 360, 432, 576, 648.\(\frac{387}{8}\) has remainder = 3; \(\frac{387}{9}\) has remainder 0. \(\frac{493}{8}\) has remainder 5; \(\frac{493}{9}\) has remainder 7. \(\frac{502}{8}\) has remainder 6; \(\frac{502}{9}\) has remainder 7. \(\frac{441}{8}\) has remainder 1; \(\frac{441}{9}\) has remainder 0. \(\frac{634}{8}\) has remainder 2; \(\frac{634}{9}\) has remainder 4. Hence 502 is the answer. |
| 45. |
 In the figure, DE//BC: DB//FE: DE = 2cm, FC = 3cm, AE = 4cm. Determine the length of EC. A. 4cm B. 6cm C. 3cm D. 2cm E. 1cm Detailed SolutionAngles ADE and EFC are similar,Therefore, = \(\frac{x}{3} = \frac{4}{2}\) = \(\frac{x}{3} = 2\) x = 3 x 2 = 6 |
|
| 46. |
 In the figure, AB is parallel to CD then x + y + z is A. 185o B. 200o C. 270o D. 360o E. 195o Detailed Solutionx + y + z = 360o |
|
| 47. |
 In the Figure FD\\AC, the area of AEF = 6sq.cm. AE = 3cm, BC = 3cm, CD = 5cm, < BCD is an obtuse angle. Find the length of BD. A. \(\sqrt{33}\) B. 6 C. 4 D. 2\(\sqrt{13}\) E. 4\(\sqrt{5}\) Detailed SolutionArea of triangle AEF = 6sq. cmarea of triangle = \(\frac{1}{2}\)bh (Line DX makes right angles with the parallel lines) 6 = \(\frac{1}{2}\) x 3 x h 6 = 3h 3h = \(\frac{12}{3}\) h = 4 = DX From D, C x D, CX2 = 52 - 42 = 25 - 16 = 9 Cx = 3. From angle B x D, Bx = 6(i.e. 3 + 3) BD2 = 42 + 62 = 16 + 36 = 52 BD = \(\sqrt{4 \times 13}\) |
|
| 48. |
 In the figure, 0 is the centre of the circle ABC, < CED = 30o, < EDA = 40o. What is the size of < ABC? A. 70o B. 110o C. 130o D. 125o E. 145o Detailed SolutionIf < CED = 30o, and < EDA = 40o then < ABC = 125o |