Year : 
2015
Title : 
Mathematics (Core)
Exam : 
WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

21 - 30 of 45 Questions

# Question Ans
21.

PQRT is square. If x is the midpoint of PQ, Calculate correct to the nearest degree, LPXS

A. 53o

B. 55o

C. 63o

D. 65o

Detailed Solution

In the diagram given,

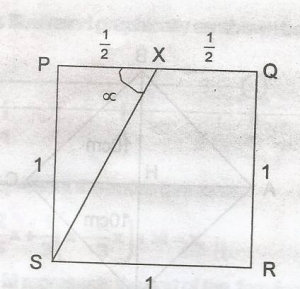tan\(\alpha\) = \(\frac{1}{0.5}\) = 2

\(\alpha\) = tan - 1(2) = 63.43o

= 63o
22.

The angle of elevation of an aircraft from a point K on the horizontal ground 30\(\alpha\). If the aircraft is 800m above the ground, how far is it from K?

A. 400.00m

B. 692.82m

C. 923.76m

D. 1,600.99m

Detailed Solution

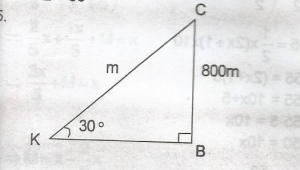In \(\bigtriangleup\)KBC, sin 30 = \(\frac{800}{IKCI}\)

IKCL = \(\frac{800}{sin30^o}\)

= \(\frac{800}{0.5}\)

= 1600m
23.

The population of students in a school is 810. If this is represented on a pie chart, calculate the sectoral angle for a class of 7 students

A. 32o

B. 45o

C. 60o

D. 75o

Detailed Solution

In a school with students' population 810, the sectoral angle for a class of 7 students is

= \(\frac{72}{810}\) x 360o

= 32o
24.

The scores of twenty students in a test are as follows: 44, 47, 48, 49, 50, 51, 52, 53, 53, 54, 58, 59, 60, 61, 63, 65, 67, 70, 73, 75. Find the third quartile.

A. 62

B. 63

C. 64

D. 65

Detailed Solution

Third quartile Q3 = \(\frac{3}{4}\)Nth

= \(\frac{3}{4}\) x 20th score

= 15th score

= 63
25.

\(\begin{array}{c|c}
Scores & 0 - 4 & 5 - 9 & 10 - 14\\
\hline Frequency & 2 & 1 & 2\end{array}\)

The table shows the distribution of the scores of some students in a test. Calculate the mean scores.

A. 5.6

B. 6.2

C. 6.6

D. 7.0

Detailed Solution

To calculate the mean of grouped data,
- First step to determine the midpoint (x) of each interval or class.
0 - 4 ►2
5 - 9 ► 7
10 - 14 ►12
These midpoints must then be multiplied by the frequencies of the corresponding classes:
2 X 2 = 4
1 X 7 = 7
2 X 12 = 24
Mean = ( 24 + 7 + 4) ÷ ( 2 + 1 + 2 )
: Mean = 7
26.

The probability that kebba, Ebou and Omar will hit a target are \(\frac{2}{3}\), \(\frac{3}{4}\) and \(\frac{4}{5}\) respectively. Find the probability that only Kebba will hit the target.

A. \(\frac{2}{5}\)

B. \(\frac{7}{60}\)

C. \(\frac{1}{30}\)

D. \(\frac{1}{60}\)

Detailed Solution

Hence the probability that only Kebba will hit the target

= P(K)xP(E')xP(O')

= \(\frac{2}{3} \times \frac{1}{4} \times \frac{1}{5}\)

= \(\frac{1}{30}\)
27.

In the diagram, VW//YZ, |WX| = 6cm, |XY| = 16cm, |YZ| = 20cm and |ZX| = 12cm. Calculate |VX|

A. 3cm

B. 4cm

C. 6cm

D. 8cm

Detailed Solution

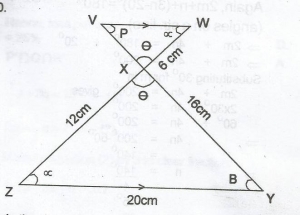In the diagram, \(\frac{16}{12} = \frac{VX}{6}\) (similar \(\Delta\)s)

VX = \(\frac{16 \times 6}{12}\)

= 8cm
28.

Tom will be 25 years old in n years' time. If he is 5 years younger than Bade's present age.

A. (30 - n)years

B. (20 - n)years

C. (25 - n)years

D. (30 + n)years

Detailed Solution

Let Tom's present agr be x.

Then x = 25 - n

If Tom is 5 years younger than Bade, then Bade's present age is x + 5 = 25 - n + 5

= (30 - n)
29.

If \(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) is simplified as m + n\(\sqrt{6}\), find the value of (m + n)

A. \(\frac{1}{3}\)

B. \(\frac{2}{3}\)

C. 1\(\frac{1}{3}\)

D. 1\(\frac{2}{3}\)

Detailed Solution

\(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) = \(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\)

= \(\frac{\sqrt{2} \times \sqrt{3} + \sqrt{3} \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)

= \(\frac{\sqrt{6} + 3}{3}\)

= \(\frac{3 + \sqrt{6}}{3}\)

= Hence, (m + n) = 1 + \(\frac{1}{3}\)


= 1\(\frac{1}{3}\)
30.

In the given diagram, \(\bar{QT}\) and \(\bar{PR}\) are straight lines, < ROS = (3n - 20), < SOT = n, < POL = m and < QOL is a right angle. Find the value of n.

A. 35o

B. 40o

C. 55o

D. 60o

Detailed Solution

In the diagram, QOR + 2m(vertically opposite angles)

So, m + 90° + 2m = 180°

(angles on str. line)

3m = 180° - 90°

3m = 90°

m = \(\frac{90^o}{3}\)

= 30°

substituting 30° for m in

2m + 4n = 200° gives

2 x 30° + 4n = 200°

60° + 4n = 200°

4n = 200° - 60°

= 140°

n = \(\frac{140°}{4}\)
<
21.

PQRT is square. If x is the midpoint of PQ, Calculate correct to the nearest degree, LPXS

A. 53o

B. 55o

C. 63o

D. 65o

Detailed Solution

In the diagram given,

tan\(\alpha\) = \(\frac{1}{0.5}\) = 2

\(\alpha\) = tan - 1(2) = 63.43o

= 63o
22.

The angle of elevation of an aircraft from a point K on the horizontal ground 30\(\alpha\). If the aircraft is 800m above the ground, how far is it from K?

A. 400.00m

B. 692.82m

C. 923.76m

D. 1,600.99m

Detailed Solution

In \(\bigtriangleup\)KBC, sin 30 = \(\frac{800}{IKCI}\)

IKCL = \(\frac{800}{sin30^o}\)

= \(\frac{800}{0.5}\)

= 1600m
23.

The population of students in a school is 810. If this is represented on a pie chart, calculate the sectoral angle for a class of 7 students

A. 32o

B. 45o

C. 60o

D. 75o

Detailed Solution

In a school with students' population 810, the sectoral angle for a class of 7 students is

= \(\frac{72}{810}\) x 360o

= 32o
24.

The scores of twenty students in a test are as follows: 44, 47, 48, 49, 50, 51, 52, 53, 53, 54, 58, 59, 60, 61, 63, 65, 67, 70, 73, 75. Find the third quartile.

A. 62

B. 63

C. 64

D. 65

Detailed Solution

Third quartile Q3 = \(\frac{3}{4}\)Nth

= \(\frac{3}{4}\) x 20th score

= 15th score

= 63
25.

\(\begin{array}{c|c}
Scores & 0 - 4 & 5 - 9 & 10 - 14\\
\hline Frequency & 2 & 1 & 2\end{array}\)

The table shows the distribution of the scores of some students in a test. Calculate the mean scores.

A. 5.6

B. 6.2

C. 6.6

D. 7.0

Detailed Solution

To calculate the mean of grouped data,
- First step to determine the midpoint (x) of each interval or class.
0 - 4 ►2
5 - 9 ► 7
10 - 14 ►12
These midpoints must then be multiplied by the frequencies of the corresponding classes:
2 X 2 = 4
1 X 7 = 7
2 X 12 = 24
Mean = ( 24 + 7 + 4) ÷ ( 2 + 1 + 2 )
: Mean = 7
26.

The probability that kebba, Ebou and Omar will hit a target are \(\frac{2}{3}\), \(\frac{3}{4}\) and \(\frac{4}{5}\) respectively. Find the probability that only Kebba will hit the target.

A. \(\frac{2}{5}\)

B. \(\frac{7}{60}\)

C. \(\frac{1}{30}\)

D. \(\frac{1}{60}\)

Detailed Solution

Hence the probability that only Kebba will hit the target

= P(K)xP(E')xP(O')

= \(\frac{2}{3} \times \frac{1}{4} \times \frac{1}{5}\)

= \(\frac{1}{30}\)
27.

In the diagram, VW//YZ, |WX| = 6cm, |XY| = 16cm, |YZ| = 20cm and |ZX| = 12cm. Calculate |VX|

A. 3cm

B. 4cm

C. 6cm

D. 8cm

Detailed Solution

In the diagram, \(\frac{16}{12} = \frac{VX}{6}\) (similar \(\Delta\)s)

VX = \(\frac{16 \times 6}{12}\)

= 8cm
28.

Tom will be 25 years old in n years' time. If he is 5 years younger than Bade's present age.

A. (30 - n)years

B. (20 - n)years

C. (25 - n)years

D. (30 + n)years

Detailed Solution

Let Tom's present agr be x.

Then x = 25 - n

If Tom is 5 years younger than Bade, then Bade's present age is x + 5 = 25 - n + 5

= (30 - n)
29.

If \(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) is simplified as m + n\(\sqrt{6}\), find the value of (m + n)

A. \(\frac{1}{3}\)

B. \(\frac{2}{3}\)

C. 1\(\frac{1}{3}\)

D. 1\(\frac{2}{3}\)

Detailed Solution

\(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) = \(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{3}}\) x \(\frac{\sqrt{3}}{\sqrt{3}}\)

= \(\frac{\sqrt{2} \times \sqrt{3} + \sqrt{3} \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)

= \(\frac{\sqrt{6} + 3}{3}\)

= \(\frac{3 + \sqrt{6}}{3}\)

= Hence, (m + n) = 1 + \(\frac{1}{3}\)


= 1\(\frac{1}{3}\)
30.

In the given diagram, \(\bar{QT}\) and \(\bar{PR}\) are straight lines, < ROS = (3n - 20), < SOT = n, < POL = m and < QOL is a right angle. Find the value of n.

A. 35o

B. 40o

C. 55o

D. 60o

Detailed Solution

In the diagram, QOR + 2m(vertically opposite angles)

So, m + 90° + 2m = 180°

(angles on str. line)

3m = 180° - 90°

3m = 90°

m = \(\frac{90^o}{3}\)

= 30°

substituting 30° for m in

2m + 4n = 200° gives

2 x 30° + 4n = 200°

60° + 4n = 200°

4n = 200° - 60°

= 140°

n = \(\frac{140°}{4}\)
<