Year :
2008
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
31 - 40 of 45 Questions
| # | Question | Ans |
|---|---|---|
| 31. |
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is picked at random from each of the two sets, what is the probability that their difference is odd? A. 1 B. \(\frac{3}{4}\) C. \(\frac{1}{4}\) D. zero Detailed Solution\(\begin{array}{c|c} x & 2 & 3 & 5 & 9 \\ \hline 2 & 4 & 6 & 10 & 18 \\ \hline 4 & 8 & 12 & 20 & 36 \\ \hline 6 & 12 & 18 & 30 & 54 \\ \hline 8 & 16 & 24 & 40 & 72 \end{array}\)Note: A {horizontal} B {vertical} Pr (Odd Product) = \(\frac{0}{16}\) = 0 |
|
| 32. |
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is picked at random from each of the two sets, what is the probability that their difference is 6 or 7? A. \(\frac{1}{256}\) B. \(\frac{1}{16}\) C. \(\frac{1}{8}\) D. \(\frac{1}{2}\) Detailed Solution\(\begin{array}{c|c} - & 2 & 3 & 5 & 9 \\ \hline 2 & 0 & 1 & 3 & 7 \\ \hline 4 & 2 & 1 & 1 & 5\\ \hline 6 & 4 & 3 & 1 & 3 \\ \hline 8 & 6 &5 & 3 & 1 \end{array}\)Note: A {horizontal} B {vertical} Pr(Difference of 6 or 7) = \(\frac{2}{16} = \frac{1}{8}\) |
|
| 33. |
Find the mean deviation of these numbers 10, 12, 14, 15, 17, 19. A. 2.5 B. 2.6 C. 2.7 D. 2.8 Detailed Solution\(\begin{array}{c|c} x & d = x - \bar{x} & |d| \\ \hline 10 & -4.5 & 4.5 \\ 12 & -2.5 & 2.5\\ 14 & -0.5 & 0.5\\ 15 & 0.5 & 0.5\\ 17 & 2.5 & 2.5\\ 19 & 4.5 & 4.5\\ \hline \sum x = 87 & & \sum|d| = 15\end{array}\)\(\bar{x} = \frac{\sum x}{n}\) = \(\frac{87}{6}\) = 14.5 |
|
| 34. |
 In the diagram, < QPR = 90o. If q2 = 25 - r2. Find the value of p A. 3 B. 4 C. 5 D. 6 Detailed SolutionGiven q2 = 25 - r2.....(1)from Pythagoras theorem p2 = q2 + r2....(2) put(1) into (2) p2 = 25 - r2 + r2 p2 = 25 p = \(\sqrt{25}\) |
|
| 35. |
 In the diagram, /PQ/ = /QR/ and /PR/ = /RS/ = /SP/, calculate the side of < QRS A. 150o B. 120o C. 90o D. 60o Detailed Solution
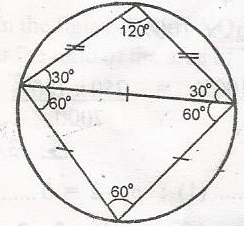 \(\bigtriangleup\) PRS is equilateral and so < RPS = < PRS = < PSR = 70o But < PQR + < PSR = 180o (Opposite interior angles of a cyclic quadrilateral) < PQR + 60 = 180o < PR = 180 - 60 = 120o But in \(\bigtriangleup\) PQR, PQ = PR, hence < QPR = < PRQ(Base angles of an Isosceles triangle) < QPR + |
|
| 36. |
In the diagram, PQRS is a rhombus. /PR/ = 10cm and /QS/ = 24cm. Calculate the perimeter of the rhombus A. 34cm B. 52cm C. 56cm D. 96cm Detailed SolutionFor a rhombus, all the sides are equal and diagonals bisect each other at 90o. Hence, the triangles formed are congruent: (under RHS).Thus: \(\bar{PS}^2\) = 52 + 122 \(\bar{PS} = \sqrt{25 + 144}\) = \(\sqrt{169}\) \(\bar{PS}\) = 13cm perimeter = 4 x length of a side = 4 x 13cm = 52cm |
|
| 37. |
 In the figure shown, PQs is a straight line. What is the value of < PRQ? A. 128o B. 108o C. 98o D. 78o Detailed Solution< QPR + < PRQ = < RQS(Sum of two interior angles of a triangle = Opposite exterior angles) 70o + < PRQ = 148 < PRQ = 148o - 70o = 78o |
|
| 38. |
 In the diagram, PQ//RS, QU//PT and < PSR = 42o. Find angle x. A. 84o B. 48o C. 42o D. 32o Detailed SolutionFrom the diagram, < QPS = xo (Corresponding angles)Also, < QPS = < PSR(Alternate angles) x = 42o |
|
| 39. |
 In the figure /PX/ = /XQ/, PQ//YZ and XV//QR. What is the ratio of the area of XYZQ to te area of \(\bigtriangleup\)YZR? A. 1:2 B. 2:1 C. 1:2 D. 3:1 Detailed SolutionFrom the diagram, XYZQ is a parallelogram. Thus, |YZ| = |XQ| = |PX|; \(\bigtriangleup\)PXY, Let the area of XYZQ = A1, the area of \(\bigtriangleup\)PXY= Area of \(\bigtriangleup\)YZR = A2 Area of \(\bigtriangleup\)PQR = A = A1 + 2A2 But from similarity of triangles \(\frac{\text{Area of PQR}}{\text{Area of PXY}} = (\frac{PQ}{PX})^2 = (\frac{QR}{XY})^2\) \(\frac{A}{A_2} = (\frac{2}{1})^2 = \frac{2}{1}\) A = 4A2 But, A = A1 + 2A A< |
|
| 40. |
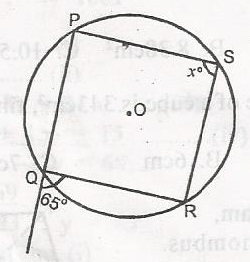 In the diagram, O is the centre of the circle and PQRS is a cyclic quadrilateral. Find the value of x. A. 25o B. 65o C. 115o D. 130o Detailed Solutionx = 65o (An interior angle of a cyclic quadrilateral = opposite exterior angle). |
| 31. |
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is picked at random from each of the two sets, what is the probability that their difference is odd? A. 1 B. \(\frac{3}{4}\) C. \(\frac{1}{4}\) D. zero Detailed Solution\(\begin{array}{c|c} x & 2 & 3 & 5 & 9 \\ \hline 2 & 4 & 6 & 10 & 18 \\ \hline 4 & 8 & 12 & 20 & 36 \\ \hline 6 & 12 & 18 & 30 & 54 \\ \hline 8 & 16 & 24 & 40 & 72 \end{array}\)Note: A {horizontal} B {vertical} Pr (Odd Product) = \(\frac{0}{16}\) = 0 |
|
| 32. |
Given the sets A = [2, 4, 6, 8] and B = [2, 3, 5, 9]. If a number is picked at random from each of the two sets, what is the probability that their difference is 6 or 7? A. \(\frac{1}{256}\) B. \(\frac{1}{16}\) C. \(\frac{1}{8}\) D. \(\frac{1}{2}\) Detailed Solution\(\begin{array}{c|c} - & 2 & 3 & 5 & 9 \\ \hline 2 & 0 & 1 & 3 & 7 \\ \hline 4 & 2 & 1 & 1 & 5\\ \hline 6 & 4 & 3 & 1 & 3 \\ \hline 8 & 6 &5 & 3 & 1 \end{array}\)Note: A {horizontal} B {vertical} Pr(Difference of 6 or 7) = \(\frac{2}{16} = \frac{1}{8}\) |
|
| 33. |
Find the mean deviation of these numbers 10, 12, 14, 15, 17, 19. A. 2.5 B. 2.6 C. 2.7 D. 2.8 Detailed Solution\(\begin{array}{c|c} x & d = x - \bar{x} & |d| \\ \hline 10 & -4.5 & 4.5 \\ 12 & -2.5 & 2.5\\ 14 & -0.5 & 0.5\\ 15 & 0.5 & 0.5\\ 17 & 2.5 & 2.5\\ 19 & 4.5 & 4.5\\ \hline \sum x = 87 & & \sum|d| = 15\end{array}\)\(\bar{x} = \frac{\sum x}{n}\) = \(\frac{87}{6}\) = 14.5 |
|
| 34. |
 In the diagram, < QPR = 90o. If q2 = 25 - r2. Find the value of p A. 3 B. 4 C. 5 D. 6 Detailed SolutionGiven q2 = 25 - r2.....(1)from Pythagoras theorem p2 = q2 + r2....(2) put(1) into (2) p2 = 25 - r2 + r2 p2 = 25 p = \(\sqrt{25}\) |
|
| 35. |
 In the diagram, /PQ/ = /QR/ and /PR/ = /RS/ = /SP/, calculate the side of < QRS A. 150o B. 120o C. 90o D. 60o Detailed Solution
 \(\bigtriangleup\) PRS is equilateral and so < RPS = < PRS = < PSR = 70o But < PQR + < PSR = 180o (Opposite interior angles of a cyclic quadrilateral) < PQR + 60 = 180o < PR = 180 - 60 = 120o But in \(\bigtriangleup\) PQR, PQ = PR, hence < QPR = < PRQ(Base angles of an Isosceles triangle) < QPR + |
| 36. |
In the diagram, PQRS is a rhombus. /PR/ = 10cm and /QS/ = 24cm. Calculate the perimeter of the rhombus A. 34cm B. 52cm C. 56cm D. 96cm Detailed SolutionFor a rhombus, all the sides are equal and diagonals bisect each other at 90o. Hence, the triangles formed are congruent: (under RHS).Thus: \(\bar{PS}^2\) = 52 + 122 \(\bar{PS} = \sqrt{25 + 144}\) = \(\sqrt{169}\) \(\bar{PS}\) = 13cm perimeter = 4 x length of a side = 4 x 13cm = 52cm |
|
| 37. |
 In the figure shown, PQs is a straight line. What is the value of < PRQ? A. 128o B. 108o C. 98o D. 78o Detailed Solution< QPR + < PRQ = < RQS(Sum of two interior angles of a triangle = Opposite exterior angles) 70o + < PRQ = 148 < PRQ = 148o - 70o = 78o |
|
| 38. |
 In the diagram, PQ//RS, QU//PT and < PSR = 42o. Find angle x. A. 84o B. 48o C. 42o D. 32o Detailed SolutionFrom the diagram, < QPS = xo (Corresponding angles)Also, < QPS = < PSR(Alternate angles) x = 42o |
|
| 39. |
 In the figure /PX/ = /XQ/, PQ//YZ and XV//QR. What is the ratio of the area of XYZQ to te area of \(\bigtriangleup\)YZR? A. 1:2 B. 2:1 C. 1:2 D. 3:1 Detailed SolutionFrom the diagram, XYZQ is a parallelogram. Thus, |YZ| = |XQ| = |PX|; \(\bigtriangleup\)PXY, Let the area of XYZQ = A1, the area of \(\bigtriangleup\)PXY= Area of \(\bigtriangleup\)YZR = A2 Area of \(\bigtriangleup\)PQR = A = A1 + 2A2 But from similarity of triangles \(\frac{\text{Area of PQR}}{\text{Area of PXY}} = (\frac{PQ}{PX})^2 = (\frac{QR}{XY})^2\) \(\frac{A}{A_2} = (\frac{2}{1})^2 = \frac{2}{1}\) A = 4A2 But, A = A1 + 2A A< |
|
| 40. |
 In the diagram, O is the centre of the circle and PQRS is a cyclic quadrilateral. Find the value of x. A. 25o B. 65o C. 115o D. 130o Detailed Solutionx = 65o (An interior angle of a cyclic quadrilateral = opposite exterior angle). |