Year :
1998
Title :
Mathematics (Core)
Exam :
WASSCE/WAEC MAY/JUNE
Paper 1 | Objectives
21 - 30 of 63 Questions
| # | Question | Ans |
|---|---|---|
| 21. |
If h(m+n) = m(h+r) find h in terms of m, n and r A. \(h=\frac{mr}{2m+n}\) B. \(h=\frac{mr}{n+m}\) C. \(h=\frac{m+n}{n}\) D. \(h=\frac{m+n}{m}\) E. \(h=\frac{mr}{n}\) Detailed Solution\(h(m+n) = m(h+r)\\hm+hn=hm+mr\\ hn=mr\\ h=\frac{mr}{n}\) |
|
| 22. |
Given that \(\frac{6x-y}{x+2y}=2\), find the value of \(\frac{x}{y}\) A. \(\frac{3}{8}\) B. \(\frac{5}{8}\) C. \(\frac{4}{5}\) D. \(\frac{5}{4}\) E. \(\frac{8}{5}\) |
D |
| 23. |
The radius of a geographical globe is 60cm. Find the length of the parallel of latitude 60oN A. \(66\pi cm\) B. \(60\pi cm\) C. \(30\pi cm\) D. \(15\pi cm\) E. \(6\pi cm\) |
B |
| 24. |
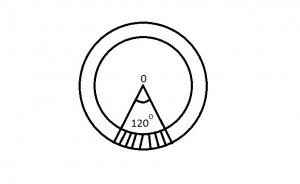 In the diagram above, O is the center if the two concentric circle of radii 13cm and 10cm respectively. Find the area of the shaded portion in the sector with angle 1200 at the center A. \(\frac{1}{3}\pi cm^2\) B. \(\pi cm^2\) C. \(3\pi cm^2\) D. \(23\pi cm^2\) E. \(46\pi cm^2\) Detailed Solution\(\frac{120\pi}{360}(R^2 - r^2)\\\frac{1}{3}\times \pi (13^2 - 10^2)\\ \frac{1}{3}\times \pi \times 69 = 23\pi cm^2\) |
|
| 25. |
Express as a single fraction: \(\frac{x}{x-2}-\frac{x+2}{x+3}\) A. \(\frac{2x^2 - 3x - 4}{(x-2)(x+3)}\) B. \(\frac{2x^2 + 3x - 4}{(x-2)(x+3)}\) C. \(\frac{2}{(x-2)(x+3)}\) D. \(\frac{ 3x + 4}{(x-2)(x+3)}\) E. \(\frac{3x - 4}{(x-2)(x+3)}\) Detailed Solution\(\frac{x}{x-2}-\frac{x+2}{x+3}\)\(\frac{[x][x+3] - [x+2][x-2]}{[x-2][x+3]}\) = \(\frac{x^2 + 3x - x^2 - 4}{[x-2][x+3]}\) = \(\frac{3x - 4}{[x-2][x+3]}\) |
|
| 26. |
The following numbers represent at a set of scores for a class of 32 students, where the maximum score possible was 12, 6, 5, 9, 4, 4, 8, 7, 5, 6, 3, 2, 5, 4, 6, 9, 10, 4, 3, 2, 3, 4, 6, 8, 7, 4, 2, 1, 8, 7, 7, 6, 11. What is the percentage of the class, correct to the nearest whole number, scored above 6? A. 34% B. 35% C. 37% D. 38% E. 50% |
D |
| 27. |
A die with faces numbered 1 to 6 is rolled once. What is the probability of obtaining 4? A. \(\frac{1}{36}\) B. \(\frac{1}{6}\) C. \(\frac{1}{3}\) D. \(\frac{1}{2}\) E. \(\frac{2}{3}\) Detailed SolutionWhen the die is rolled, occasion of getting 4P(obtaining a 4) = \(\frac{1}{6}\) = \(\frac{1}{6}\) |
|
| 28. |
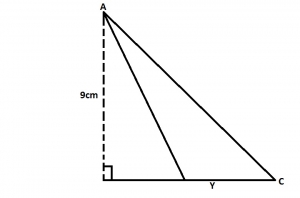 In the diagram above, the area of triangle ABC is 35cm2, find the value of y A. 5cm B. 10cm C. 17.5cm D. 28cm E. 70cm |
B |
| 29. |
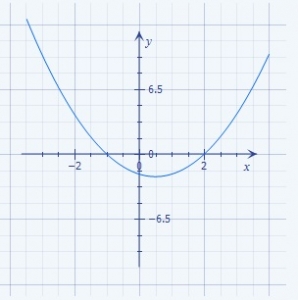 The graph of the quadratic expression A. \(y=x^2 + x - 2\) B. \(y=x^2 - x + 2\) C. \(y=x^2 - x - 2\) D. \(y=x + x + 2\) E. \(y=x^2 - 2 x - 2\) |
C |
| 30. |
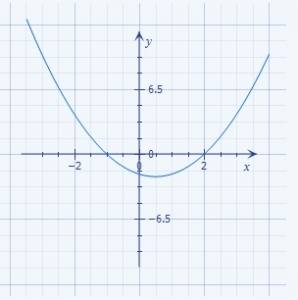 The values of x when y = -1 are approximately A. -10 and 2.0 B. -1.3 and 2.3 C. -0.6 and 2.6 D. -0.6 and 1.6 E. 1.6 and 1.6 |
D |
| 21. |
If h(m+n) = m(h+r) find h in terms of m, n and r A. \(h=\frac{mr}{2m+n}\) B. \(h=\frac{mr}{n+m}\) C. \(h=\frac{m+n}{n}\) D. \(h=\frac{m+n}{m}\) E. \(h=\frac{mr}{n}\) Detailed Solution\(h(m+n) = m(h+r)\\hm+hn=hm+mr\\ hn=mr\\ h=\frac{mr}{n}\) |
|
| 22. |
Given that \(\frac{6x-y}{x+2y}=2\), find the value of \(\frac{x}{y}\) A. \(\frac{3}{8}\) B. \(\frac{5}{8}\) C. \(\frac{4}{5}\) D. \(\frac{5}{4}\) E. \(\frac{8}{5}\) |
D |
| 23. |
The radius of a geographical globe is 60cm. Find the length of the parallel of latitude 60oN A. \(66\pi cm\) B. \(60\pi cm\) C. \(30\pi cm\) D. \(15\pi cm\) E. \(6\pi cm\) |
B |
| 24. |
 In the diagram above, O is the center if the two concentric circle of radii 13cm and 10cm respectively. Find the area of the shaded portion in the sector with angle 1200 at the center A. \(\frac{1}{3}\pi cm^2\) B. \(\pi cm^2\) C. \(3\pi cm^2\) D. \(23\pi cm^2\) E. \(46\pi cm^2\) Detailed Solution\(\frac{120\pi}{360}(R^2 - r^2)\\\frac{1}{3}\times \pi (13^2 - 10^2)\\ \frac{1}{3}\times \pi \times 69 = 23\pi cm^2\) |
|
| 25. |
Express as a single fraction: \(\frac{x}{x-2}-\frac{x+2}{x+3}\) A. \(\frac{2x^2 - 3x - 4}{(x-2)(x+3)}\) B. \(\frac{2x^2 + 3x - 4}{(x-2)(x+3)}\) C. \(\frac{2}{(x-2)(x+3)}\) D. \(\frac{ 3x + 4}{(x-2)(x+3)}\) E. \(\frac{3x - 4}{(x-2)(x+3)}\) Detailed Solution\(\frac{x}{x-2}-\frac{x+2}{x+3}\)\(\frac{[x][x+3] - [x+2][x-2]}{[x-2][x+3]}\) = \(\frac{x^2 + 3x - x^2 - 4}{[x-2][x+3]}\) = \(\frac{3x - 4}{[x-2][x+3]}\) |
| 26. |
The following numbers represent at a set of scores for a class of 32 students, where the maximum score possible was 12, 6, 5, 9, 4, 4, 8, 7, 5, 6, 3, 2, 5, 4, 6, 9, 10, 4, 3, 2, 3, 4, 6, 8, 7, 4, 2, 1, 8, 7, 7, 6, 11. What is the percentage of the class, correct to the nearest whole number, scored above 6? A. 34% B. 35% C. 37% D. 38% E. 50% |
D |
| 27. |
A die with faces numbered 1 to 6 is rolled once. What is the probability of obtaining 4? A. \(\frac{1}{36}\) B. \(\frac{1}{6}\) C. \(\frac{1}{3}\) D. \(\frac{1}{2}\) E. \(\frac{2}{3}\) Detailed SolutionWhen the die is rolled, occasion of getting 4P(obtaining a 4) = \(\frac{1}{6}\) = \(\frac{1}{6}\) |
|
| 28. |
 In the diagram above, the area of triangle ABC is 35cm2, find the value of y A. 5cm B. 10cm C. 17.5cm D. 28cm E. 70cm |
B |
| 29. |
 The graph of the quadratic expression A. \(y=x^2 + x - 2\) B. \(y=x^2 - x + 2\) C. \(y=x^2 - x - 2\) D. \(y=x + x + 2\) E. \(y=x^2 - 2 x - 2\) |
C |
| 30. |
 The values of x when y = -1 are approximately A. -10 and 2.0 B. -1.3 and 2.3 C. -0.6 and 2.6 D. -0.6 and 1.6 E. 1.6 and 1.6 |
D |