Year : 
2000
Title : 
Mathematics (Core)
Exam : 
JAMB Exam

Paper 1 | Objectives

31 - 40 of 45 Questions

# Question Ans
31.

In how many ways can the word MATHEMATICS be arranged?

A. 11!/(9! 2!)

B. 11!/(9! 2! 2!)

C. 11!/(2! 2! 2!)

D. 11!/(2! 2!)

Detailed Solution

Number of letter in MATHEMATICS = 11
Number of letter M = 2
Number of letter T = 2
Number of letter A = 2

Arrangement = 11!/(2! 2! 2!) ways
32.

Given that the various faces of a fair dice 1, 2, 3, 4, 5, 6 appeared 30, 43, 54, 40, 41, 32 times respectively in a single toss. Picture the figures as being represented in a simple table with number (X) against frequency (f).

If a pie chart is used to depict the data, the angle corresponding to 4 is?

A. 10°

B. 16°

C. 40°

D. 60°

Detailed Solution

Angle corresponding to 4 is 40/240 x 360/1 = 60°

Note that total angle in a circle is 360°.
Note also that sum of the frequencies given is 240.
33.

If U = {x : x is an integer and 1 \(\leq\) x \(\leq\) 20
E1 = {x : x is a multiple of 3}
E2 = {x : x is a multiple of 4}
and an integer is picked at random from U, find the probability that it is not in E2

A. 3/4

B. 3/10

C. 1/4

D. 1/20

Detailed Solution

U = {1, 2, 3, 4, 5,..., 20}
E1 = {3, 6, 9, 12, 15, 18}
E2 = {4, 8, 12, 16, 20}
P(E1) = 5/20
P(not E1) = 1 - (5/20) = 15/20 = 3/4
34.

The variance of x, 2x, 3x, 4x and 5x is

A. x√2

B. 2x2

C. x2

D. 3x

Detailed Solution

Hint: prepare a three-columned table, one for (x), another for the (deviation), and the last for the (squared-deviation).

Sum of (x) = 15x, algebraic sum of (deviation) = zero (0)
Sum of (squared-deviation) = 10x2

Variance = ∑(squared-deviation)/n = 10x2/5 = 2x2
35.

Find the sum of the range and the mode of the set of numbers 10, 9, 10, 9, 8, 7, 7, 10, 8, 10, 8, 4, 6, 9, 10, 9, 10, 9, 7, 10, 6, 5

A. 16

B. 14

C. 12

D. 10

Detailed Solution

Range = Highest - lowest number => 10-4 = 6
Mode is the number with highest occurrence => Mode = 10

Sum = 6 + 10 = 16
36.

In how many ways can a delegation of 3 be chosen from among 5 men and 3 women, if at least one man and at least one woman must be included?

A. 15

B. 28

C. 30

D. 45

Detailed Solution

No of ways of choosing 1 man, 2 women = 5C1 x 3C2
No of ways of choosing 2 men, 1 woman = 5C2 x 3C1
Summing, => (5C1 x 3C2) + (5C2 x 3C1) = 15 + 30 = 45
37.

A function f(x) passes through the origin and its first derivative is 3x + 2. What is f(x)?

A. y = (3x2/)2 + 2x

B. y = (3x2)/2 + x

C. y = 3x2 + (x/2)

D. y = 3x2 +2x

Detailed Solution

Hints:
1. Integrate the given first derivative of f(x) at the boundaries, (0,0)

Then solve accordingly to get f(x) = y = (3x2/)2 + 2x
38.

The expression ax2 + bx + c equals 5 at x = 1. If its derivative is 2x + 1, what are the values of a, b, c respectively?

A. 1, 3, 1

B. 1, 2, 1

C. 2, 1, 1

D. 1, 1, 3

Detailed Solution

At x = 1, substituting x = 1 in the equation: ax2 + bx + c = 5;
f(1) => a + b + c = 5 .....(1)

Taking the first derivative of f(x) in the original equation gives dy/dx = 2ax + b = 2x + 1 (given)....(2)

From (2),=> b = 1, and 2ax = 2x, => a = 1.

substituting into (1) 1 + 1 + c = 5, => c = 5 - 2 = 3

Thus a = 1, b = 1 and c = 3
39.

Evaluate 5-3log52 x 22log23

A. 8

B. 11/8

C. 2/5

D. 1/8

Detailed Solution

5-3log52 x 22log23
i Let -3log52 = p => log52-3 = p
∴2-3 = 5p
∴5-3log52 = 5log52-3 = 5p
ii 22log23 = q => log532 = q
∴32 = 2q
∴222log23<
40.

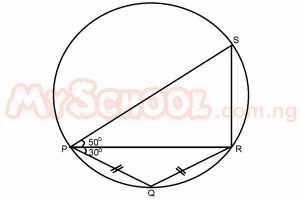In the diagram above, if ∠RPS = 50o, ∠RPQ = 30o and PQ = QR, find the value of ∠PRS.

A. 80o

B. 70o

C. 60o

D. 50o

Detailed Solution

Δ PQR is isosceles
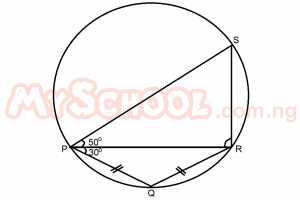∴∠PRQ = 30o
Also in Δ PQR
^Q = 180 -(30 + 30)
= 120o
PQRS is a cyclic quad
∴^S + ^Q = 180(opp ∠s of a cyclic quad)
S + 120 = 180
S = 60o
In ΔPSR
x + 50 + 60
= 180(sum of ∠s of a Δ)
x + 110 = 180
x = 180 - 110
x = 70o
31.

In how many ways can the word MATHEMATICS be arranged?

A. 11!/(9! 2!)

B. 11!/(9! 2! 2!)

C. 11!/(2! 2! 2!)

D. 11!/(2! 2!)

Detailed Solution

Number of letter in MATHEMATICS = 11
Number of letter M = 2
Number of letter T = 2
Number of letter A = 2

Arrangement = 11!/(2! 2! 2!) ways
32.

Given that the various faces of a fair dice 1, 2, 3, 4, 5, 6 appeared 30, 43, 54, 40, 41, 32 times respectively in a single toss. Picture the figures as being represented in a simple table with number (X) against frequency (f).

If a pie chart is used to depict the data, the angle corresponding to 4 is?

A. 10°

B. 16°

C. 40°

D. 60°

Detailed Solution

Angle corresponding to 4 is 40/240 x 360/1 = 60°

Note that total angle in a circle is 360°.
Note also that sum of the frequencies given is 240.
33.

If U = {x : x is an integer and 1 \(\leq\) x \(\leq\) 20
E1 = {x : x is a multiple of 3}
E2 = {x : x is a multiple of 4}
and an integer is picked at random from U, find the probability that it is not in E2

A. 3/4

B. 3/10

C. 1/4

D. 1/20

Detailed Solution

U = {1, 2, 3, 4, 5,..., 20}
E1 = {3, 6, 9, 12, 15, 18}
E2 = {4, 8, 12, 16, 20}
P(E1) = 5/20
P(not E1) = 1 - (5/20) = 15/20 = 3/4
34.

The variance of x, 2x, 3x, 4x and 5x is

A. x√2

B. 2x2

C. x2

D. 3x

Detailed Solution

Hint: prepare a three-columned table, one for (x), another for the (deviation), and the last for the (squared-deviation).

Sum of (x) = 15x, algebraic sum of (deviation) = zero (0)
Sum of (squared-deviation) = 10x2

Variance = ∑(squared-deviation)/n = 10x2/5 = 2x2
35.

Find the sum of the range and the mode of the set of numbers 10, 9, 10, 9, 8, 7, 7, 10, 8, 10, 8, 4, 6, 9, 10, 9, 10, 9, 7, 10, 6, 5

A. 16

B. 14

C. 12

D. 10

Detailed Solution

Range = Highest - lowest number => 10-4 = 6
Mode is the number with highest occurrence => Mode = 10

Sum = 6 + 10 = 16
36.

In how many ways can a delegation of 3 be chosen from among 5 men and 3 women, if at least one man and at least one woman must be included?

A. 15

B. 28

C. 30

D. 45

Detailed Solution

No of ways of choosing 1 man, 2 women = 5C1 x 3C2
No of ways of choosing 2 men, 1 woman = 5C2 x 3C1
Summing, => (5C1 x 3C2) + (5C2 x 3C1) = 15 + 30 = 45
37.

A function f(x) passes through the origin and its first derivative is 3x + 2. What is f(x)?

A. y = (3x2/)2 + 2x

B. y = (3x2)/2 + x

C. y = 3x2 + (x/2)

D. y = 3x2 +2x

Detailed Solution

Hints:
1. Integrate the given first derivative of f(x) at the boundaries, (0,0)

Then solve accordingly to get f(x) = y = (3x2/)2 + 2x
38.

The expression ax2 + bx + c equals 5 at x = 1. If its derivative is 2x + 1, what are the values of a, b, c respectively?

A. 1, 3, 1

B. 1, 2, 1

C. 2, 1, 1

D. 1, 1, 3

Detailed Solution

At x = 1, substituting x = 1 in the equation: ax2 + bx + c = 5;
f(1) => a + b + c = 5 .....(1)

Taking the first derivative of f(x) in the original equation gives dy/dx = 2ax + b = 2x + 1 (given)....(2)

From (2),=> b = 1, and 2ax = 2x, => a = 1.

substituting into (1) 1 + 1 + c = 5, => c = 5 - 2 = 3

Thus a = 1, b = 1 and c = 3
39.

Evaluate 5-3log52 x 22log23

A. 8

B. 11/8

C. 2/5

D. 1/8

Detailed Solution

5-3log52 x 22log23
i Let -3log52 = p => log52-3 = p
∴2-3 = 5p
∴5-3log52 = 5log52-3 = 5p
ii 22log23 = q => log532 = q
∴32 = 2q
∴222log23<
40.

In the diagram above, if ∠RPS = 50o, ∠RPQ = 30o and PQ = QR, find the value of ∠PRS.

A. 80o

B. 70o

C. 60o

D. 50o

Detailed Solution

Δ PQR is isosceles
∴∠PRQ = 30o
Also in Δ PQR
^Q = 180 -(30 + 30)
= 120o
PQRS is a cyclic quad
∴^S + ^Q = 180(opp ∠s of a cyclic quad)
S + 120 = 180
S = 60o
In ΔPSR
x + 50 + 60
= 180(sum of ∠s of a Δ)
x + 110 = 180
x = 180 - 110
x = 70o