Year : 
2016
Title : 
Mathematics (Core)
Exam : 
WASSCE/WAEC MAY/JUNE

Paper 1 | Objectives

41 - 49 of 49 Questions

# Question Ans
41.

A bag contains 5 red and 4 blue identical balls. Id two balls are selected at random from the bag, one after the other, with replacement, find the probability that the first is red and the second is blue

A. \(\frac{2}{9}\)

B. \(\frac{5}{18}\)

C. \(\frac{20}{81}\)

D. \(\frac{5}{9}\)

Detailed Solution

n(red balls) = 5

n(blue balls) = 4

n(\(\iff\)) = 9

Hence, prob (R1, B2)

= \(\frac{5}{9} \times \frac{4}{9}\)

= \(\frac{20}{81}\)
42.

The relation y = x2 + 2x + k passes through the point (2,0). Find the value of k

A. - 8

B. - 4

C. 4

D. 8

Detailed Solution

Y = x2 + 2x + k (given)

y = o when x = 2

thus 0 = 22 + 2 x 2 + k

0 = 4 + 4 + k

given k = -8
43.

Find the next three terms of the sequence; 0, 1, 1, 2, 3, 5, 8...

A. 13, 19, 23

B. 9, 11, 13

C. 11, 15, 19

D. 13, 21, 34

D
44.

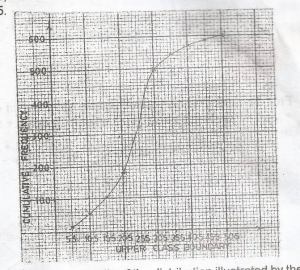Find the lower quartile of the distribution illustrated by the cumulative frequency curve

A. 17.5

B. 19.0

C. 27.5

D. 28.0

Detailed Solution

Lower quartile,

Q1 = \(\frac{1}{4}\)Nth term

= \(\frac{1}{4}\) x 600th term

= 150th term

= 15.5 + 3 + 0.5

= 19
45.

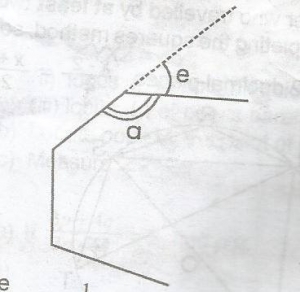
The ratio of the exterior angle to the interior angle of a regular polygon is 1:11. How many sides has the polygon?

A. 30

B. 24

C. 18

D. 12

Detailed Solution

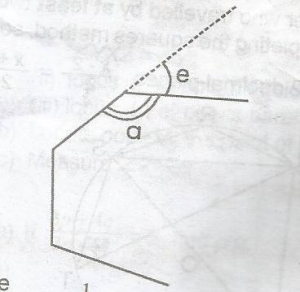Let a represent an interior angle; e represent an exterior angle. A section of the polygon is down in the diagram.

\(\frac{e}{a}\) = \(\frac{l}{11}\) given

a = 11e

a + e = 180o(angles on a straight line)

11e + e = 180o

12e = 180o

e = \(\frac{180^o}{12}\)

= 15o

Hence, number of s
46.

Halima is n years old. Her brother's age is 5 years more than half of her age. How old is her brother?

A. \(\frac{n}{2} + \frac{5}{2}\)

B. \(\frac{n}{2}\) - 5

C. 5 - \(\frac{n}{2}\)

D. \(\frac{n}{2}\) + 5

Detailed Solution

Halima's age = n years old

Her brother's age = \(\frac{n}{2}\) + 5
47.

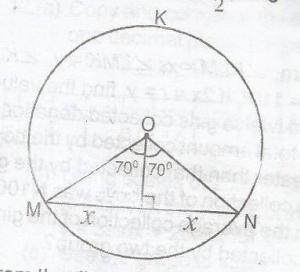
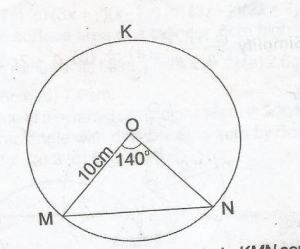In the diagram MN is a chord of a circle KMN centre O and radius 10cm. If < MON = 140o, find, correct to the nearest cm, the length of the chord MN.

A. 19cm

B. 18cm

C. 17cm

D. 12cm

Detailed Solution

From the diagram

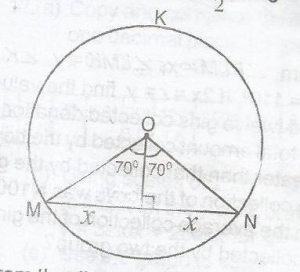sin 70o = \(\frac{x}{10}\)

x = 10sin 70o

= 9.3969

Hence, length of chord MN = 2x

= 2 x 9.3969

= 18.7938

= 19cm (nearest cm)
48.

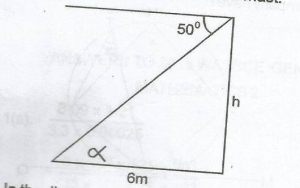
An object is 6m away from the base of a mast. If the angle of depression of the object from the top of the mast is 50o, find, correct to 2 decimal places, the height of the mast.

A. 8.60m

B. 7.83m

C. 7.51m

D. 7.15m

Detailed Solution

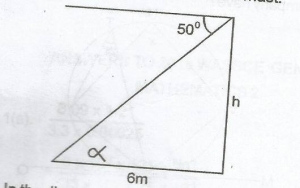In the diagram give, \(\alpha\) 50o(alternative angles)

tan\(\alpha\) = \(\frac{h}{6}\)

h = 6tan\(\alpha\)

= 6tan 50o

= 6 x 1.1918

= 7.1508

= 7.15m (2d.p)
49.

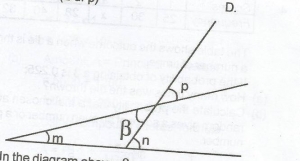
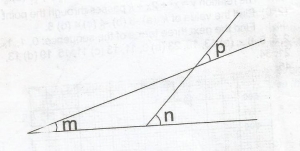From the diagram, which of the following is true?

A. m + n + p = 180o

B. m + n = 180o

C. m = p + n

D. n = m + p

Detailed Solution

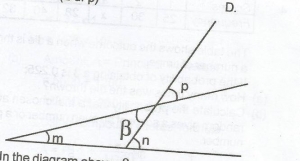In the diagram, \(\beta\) = p(vertically opposite angles)

m + \(\beta\) = n(sum of interior opp. angles)

m + p = n
41.

A bag contains 5 red and 4 blue identical balls. Id two balls are selected at random from the bag, one after the other, with replacement, find the probability that the first is red and the second is blue

A. \(\frac{2}{9}\)

B. \(\frac{5}{18}\)

C. \(\frac{20}{81}\)

D. \(\frac{5}{9}\)

Detailed Solution

n(red balls) = 5

n(blue balls) = 4

n(\(\iff\)) = 9

Hence, prob (R1, B2)

= \(\frac{5}{9} \times \frac{4}{9}\)

= \(\frac{20}{81}\)
42.

The relation y = x2 + 2x + k passes through the point (2,0). Find the value of k

A. - 8

B. - 4

C. 4

D. 8

Detailed Solution

Y = x2 + 2x + k (given)

y = o when x = 2

thus 0 = 22 + 2 x 2 + k

0 = 4 + 4 + k

given k = -8
43.

Find the next three terms of the sequence; 0, 1, 1, 2, 3, 5, 8...

A. 13, 19, 23

B. 9, 11, 13

C. 11, 15, 19

D. 13, 21, 34

D
44.

Find the lower quartile of the distribution illustrated by the cumulative frequency curve

A. 17.5

B. 19.0

C. 27.5

D. 28.0

Detailed Solution

Lower quartile,

Q1 = \(\frac{1}{4}\)Nth term

= \(\frac{1}{4}\) x 600th term

= 150th term

= 15.5 + 3 + 0.5

= 19
45.

The ratio of the exterior angle to the interior angle of a regular polygon is 1:11. How many sides has the polygon?

A. 30

B. 24

C. 18

D. 12

Detailed Solution

Let a represent an interior angle; e represent an exterior angle. A section of the polygon is down in the diagram.

\(\frac{e}{a}\) = \(\frac{l}{11}\) given

a = 11e

a + e = 180o(angles on a straight line)

11e + e = 180o

12e = 180o

e = \(\frac{180^o}{12}\)

= 15o

Hence, number of s
46.

Halima is n years old. Her brother's age is 5 years more than half of her age. How old is her brother?

A. \(\frac{n}{2} + \frac{5}{2}\)

B. \(\frac{n}{2}\) - 5

C. 5 - \(\frac{n}{2}\)

D. \(\frac{n}{2}\) + 5

Detailed Solution

Halima's age = n years old

Her brother's age = \(\frac{n}{2}\) + 5
47.

In the diagram MN is a chord of a circle KMN centre O and radius 10cm. If < MON = 140o, find, correct to the nearest cm, the length of the chord MN.

A. 19cm

B. 18cm

C. 17cm

D. 12cm

Detailed Solution

From the diagram

sin 70o = \(\frac{x}{10}\)

x = 10sin 70o

= 9.3969

Hence, length of chord MN = 2x

= 2 x 9.3969

= 18.7938

= 19cm (nearest cm)
48.

An object is 6m away from the base of a mast. If the angle of depression of the object from the top of the mast is 50o, find, correct to 2 decimal places, the height of the mast.

A. 8.60m

B. 7.83m

C. 7.51m

D. 7.15m

Detailed Solution

In the diagram give, \(\alpha\) 50o(alternative angles)

tan\(\alpha\) = \(\frac{h}{6}\)

h = 6tan\(\alpha\)

= 6tan 50o

= 6 x 1.1918

= 7.1508

= 7.15m (2d.p)
49.

From the diagram, which of the following is true?

A. m + n + p = 180o

B. m + n = 180o

C. m = p + n

D. n = m + p

Detailed Solution

In the diagram, \(\beta\) = p(vertically opposite angles)

m + \(\beta\) = n(sum of interior opp. angles)

m + p = n